WolframAlpha   Lexikon   Formelsamlingar   Terminologi länkar   Svenska matematiklänkar   Math. Resources on the Internet   Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

Logik     Mängder     Relationer     Diverse     Operationer     Geometri     Analys     Exponential- och logaritmfunktioner     Trigonometriska och hyperboliska funktioner     Komplexa tal

Logik

Symbol, tecken	Tillämpning	Benämning	Betydelse och anmärkningar
	p q	konjunktionstecken	p och q
	p q	disjunktionstecken	p eller q (eller båda)
¬	¬ p	negationstecken	negation av p; icke p
	p q	implikationstecken	om p så q; p medför q
	p q	ekvivalenstecken	p är ekvivalent med q
	x A p(x)	allkvantor (allkvantifikator)	för varje x som tillhör A gäller utsagan p(x)
	x A p(x)	existenskvantor (existenskvantifikator)	det existerar ett x som tillhör A för vilket utsagan p(x) är sann

Mängder

Symbol, tecken	Tillämpning	Betydelse, benämning,	Anmärkningar och exempel
	x A	x tillhör A x är ett element i mängden A
	y A	y tillhör inte A y är inte ett element i mängden A
	A x	mängden A innehåller x (som element)	A x har samma betydelse som x A
	A y	mängden A innehåller inte y (som element)	A y har samma betydelse som y A
{,…,}	{x1,x2,…,xn}	mängdklammer mängd med elementen x1,x2,…,xn	Kan även skrivas {xi:i I}, där I betecknar mängden av index.
{ | } eller { : }	{x A | p(x)}	mängdbyggare mängden av de element i mängden A, för vilka utsagan p(x) är sann	Exempel: {x | x ≤5 }
card	card(A)	kardinalitet; antalet element i A
Ø		tomma mängden
N		mängden av naturliga tal	Ex.: 0 = {0, 1, 2, 3, …}; * = {1, 2, 3, …}
Z		mängden av heltal	= {…, -2, -1, 0, 1, 2, …}
Q		mängden av rationella tal
R		mängden av reella tal
C		mängden av komplexa tal
[,]	[a,b]	slutet intervall i från a (inkluderat) till b (inkluderat)	[a,b] = {x | a ≤ x ≤ b}
],] (,]	]a,b] (a,b]	vänsterhalvöppet intervall i från a (exkluderat) till b (inkluderat)	]a,b] = {x | a < x ≤ b}
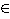[,[ [,)	[a,b[ [a,b)	högerhalvöppet intervall i från a (inkluderat) till b (exkluderat)	[a,b[ = {x | a ≤ x < b}
],[ (,)	]a,b[ (a,b)	öppet intervall i från a (exkluderat) till b (exkluderat)	]a,b[ = {x | a < x < b}
	B A	tecken för inklusion B är en delmängd av A B innehålls i A	Varje element i B tillhör A.
	B A	tecken för äkta inklusion B är en äkta delmängd av A B innehålls strängt i A	Varje element i B tillhör A, men B är inte lika med A.
	C A	tecken för icke-inklusion C är inte en delmängd av A	Symbolen används också.
	A B	tecken för inklusion A innehåller B (som delmängd) A omfattar B	A innehåller varje element i B
	A B	tecken för äkta inklusion A innehåller B som äkta delmängd	A innehåller varje element i B, men A är inte lika med B.
	A C	tecken för icke-inklusion A innehåller inte C (som delmängd)
	A B	tecken för union unionen av A och B A union B	A B = {x | x A x B} Mängden av element som tillhör A eller B eller både A och B
		tecken för union unionen av mängderna A1, A2, … , An	= A1 A2 … An mängden av element som tillhör minst en av mängderna A1, … An
∩	A ∩ B	tecken för snitt snittet av A och B A snitt B	A ∩ B = {x | x A x B} Mängden av alla element som tillhör både A och B
		tecken för snitt snittet av mängderna A1, A2, … , An	= A1 ∩ A2 ∩ … ∩ An mängden av element som tillhör alla mängderna A1, A2, … An
\	A \ B	tecken för differens av mängder differensen av A och B; A differens B	Mängden av element som tillhör A, men inte B. A \ B = {x | x A x B} A - B bör inte användas.
	AB	tecken för komplement komplementet till delmängden B av A	Mängden av de element tillhörande mängden A som inte tillhör delmängden B. Även AB = A \ B
( , )	(a, b)	ordnat par a, b	(a, b) = (c, d) om och endast om a = c och b = d a, b används också.
( ,…, )	(a1, a2, … an)	ordnad n-tipel	a1, a2, … an används också.
×	A × B	tecken för produkt av mängder kartesiska produkten av A och B A kryss B	Mängden av ordnade par (a, b) sådana att a A och b B. A × B = {(a, b) | a A b B}
Δ	ΔA	mängden av par (x, x) i A × A, där x A; diagonalen till mängden A × A	ΔA = {(x, x) | x A} idA används också.

Jämförelse, relationer

Symbol, tecken	Tillämpning	Benämning, betydelse,	Anmärkning och exempel
=	a = b	likhetstecken a är lika med b
≡		identitetstecken … är identisk med …	sin(π/2 - x) ≡ cos x
≠	a ≠ b	olikhetstecken a är inte lika med b
≈		approximationstecken … är ungefär lika med …	π ≈ 3,14
~	a ~ b a b	proportionalitetstecken a är proportionell mot b	(tecknet används mycket sällan) i geometri: är likformig med
<	a < b	a är mindre än b	olikhetstecken
>	b > a	b är större än a	olikhetstecken
≤	a ≤ b	a är mindre än eller lika med b	olikhetstecken
≥	b ≥ a	b är större än eller lika med a	olikhetstecken
	a b	a är mycket mindre än b	olikhetstecken
	b a	b är mycket större än a	olikhetstecken
	a b	a motsvarar b	t ex: Då 1 cm på en karta motsvarar en längd av 10 km, kan man skriva 1 cm 10 km

Diverse tecken och symboler

Symbol, tecken	Tillämpning	Benämning, betydelse	Anmärkningar och exempel
	a  b	a är definitionsmässigt lika med b	Ex: p mv, där p är rörelsemängd, m är massa och v är hastighet.
…	1, 2, 3, … n	utelämningstecken och så
	a = b  b = a	alltså (är)
		varav följer,
∞		oändlighetstecken
(  )	(a + b)c	ac + bc parentes, rundparentes	I vanlig algebra är ordningen av ( ), [ ], { } och   i sammansatt uttryck inte standardiserad. Inom vissa områden har ( ), [ ], { } och   särskilda betydelser.
[  ]	[a + b]c	ac + bc hakparentes
{  }	{a + b}c	ac + bc spetsparentes
	a + bc	vinkelparentes

Operationer

Symbol, tecken	Tillämpning	Benämning, betydelse	Anmärkningar och exempel
+	a + b	plustecken a plus b addition, positiv term
−	a - b	minustecken a minus b subtraktion, negativ term
±	a ± b	plusminustecken a plus eller minus b
	a b	minusplustecken a minus eller plus b	- (a ± b) = - a  b
∆	∆x = x1 - x2	delta differens, tillskott (inkrement)
·	a·b    ab	multiplikationstecken a multiplicerat med b; a gånger b multiplikation	Tecknet för multiplikation av tal är ett kryss (×) eller en halvhög punkt (·).
×	210 mm × 297 mm	kryss, Andreas-kors multiplikationstecken för mått och vektorprodukt	I det fall att punkt användas som decimaltecken skall endast krysset användas för multiplikation av tal.
⁄	a/b	snett bråkstreck, divisionstecken a dividerat med b; a genom b	division tecknas även:   ab-1   a:b   a÷b
:	a:b	kolontecken för proportion eller division
∑		summatecken Summan av en följd av tal a1 + a2 + a3 + … + an
∏		produkttecken Produkten av en följd av tal a1 · a2 · a3 · … · an
ap		a upphöjt till p
√		(kvadrat)rottecken kvadratroten ur a	(     = rotstreck)   Om a ≥ 0, så ≥ 0.
		n:te roten ur a
| |	|a|	beloppstecken absolutbeloppet av a
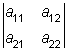| |		determinanttecken determinanten av den kvadratiska matrisen a
sgn	sgn a	signum  signum a  tecken för a	För ett reellt tal gäller: 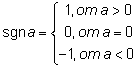För ett komplext tal:
¯ (ett rakt streck ovanpå)		medelvärde av a	Aritmetiska medelvärdet av a1 , a2 , a3 , … , an betecknas
!	n!	fakultet	Produkten av 1 · 2 · 3 · … · n skrivs n! och utläses "n-fakultet"
		binomialkoefficienten n, p; n över p
ent	ent a	det största heltal som är mindre än eller lika med a heltalsdelen av a	ent 2,4 = 2 ent(-2,4) = -3

Geometri

Symbol	Tillämpning	Betydelse, benämning,
	AB  CD	linjen AB är vinkelrät mot linjen CD
	ABCD	linjen AB är parallell med linjen CD
Δ	ΔABC	triangeln ABC
~	ΔABC ~ ΔDEF	triangeln ABC är likformig med triangeln DEF
	ΔABC ΔDEF	triangeln ABC är kongruent med triangeln DEF
	A	vinkeln A
	AB	sträckan AB
	AB	längden av AB
º, ’, ”		grader, minuter, sekunder
R	α = R	symbol för 90º (π/2 radianer) α = 90º

Analys

Symbol, Tillämpning	Betydelse, benämning	Anmärkningar och exempel
ƒ	funktionen ƒ	En funktion kan också betecknas med xƒ(x). Andra bokstäver än ƒ användas också.
ƒ(x) ƒ(x,y …)	värdet av funktion ƒ i x respektive i (x,y, …)
ƒ(x)| [ƒ(x)]	ƒ(b) - ƒ(a)	Detta beteckningssätt används huvudsakligen vid beräkning av bestämda integraler.
gƒ	den sammansatta funktionen av ƒ och g   utläses g cirkel ƒ	(gƒ) = g(ƒ(x))
x → a	x går mot a (konvergerar) konvergenstecken
limx→aƒ(x)	gränsvärdet av ƒ(x) då x går mot a.	limx→a ƒ(x) = b kan skrivas: ƒ(x) → b då x → a. Gränsvärdena "från höger" (x > a) och "från vänster" (x < a) kan betecknas limx→a+ ƒ(x) respektive limx→a− ƒ(x)
	är asymptotiskt lika med	Exempel:    då x → a.
Δx	(ändligt) tillskott till x
dƒ/dx ƒ’	derivatan av funktionen ƒ av en variabel, ƒ’ utläses ƒ-prim	Dƒ används okså. , dƒ(x)/dx,ƒ’x, Dƒx Om den oberoende variabeln är tiden t, används även istället för . utläses ƒ-prick.
(dƒ(x)/dx)x=a ƒ’(a)	värdet i a av derivatan till funktionen ƒ	Dƒ(a) används också.
dnƒ/dxn) ƒ(n)	n:te derivatan till funktionen ƒ av en variabel	Dnƒ används också. För n = 2, e används också ƒ”, ƒ”’ för ƒ(n). Om den oberoende variabeln är tiden t, används även i stället för . utläses ƒ-prick-prick.
∂ƒ/∂x ∂xƒ	partiella derivatan av funktionen ƒ av flera variabler x, y, … med avseende på x	Dxƒ används också.  ,   ∂ƒ(x, y, …)/∂x,   ∂xƒ(x, y, …)   Dxƒ(x, y, …) De övriga oberoende variablerna kan anges som index, t ex Detta beteckningssätt för partiell derivata kan utsträckas till derivator av högre ordning, t ex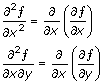
dƒ	totala differentialen av funktionen ƒ	dƒ(x, y, …) = dx + dy + …
∫ƒ(x) dx	obestämd integral av funktionen ƒ
ƒ(x) dx	bestämda integralen av funktionen ƒ från a till b	Multipelintegraler betecknas t ex: De speciella beteckningarna ∫Cƒ(x,y,z)ds ∫Sƒ(x,y,z)dA ∫Vƒ(x,y,z)dV Cƒ(x,y,z)ds används för att ange en integral: längs kurvan C (contour) med bågelementet ds, en yta S (surface) med areaelementet dA, över rymdområdet V (volume) med volumelementet dV resp längs en sluten kurva C med bågelementet ds.

Exponential- och logaritmfunktioner

Tecken, symbol uttryck	Betydelse	Anmärkningar och exempel
ax	exponentialfunktionen med basen a av x
e	basen för naturliga logaritmer
ex exp x	exponentialfunktionen (med basen e) av x
logax	logaritmen med basen a för x, a-logaritmen för x	log x används då basen inte behöver specificeras
ln x	ln x = logex; naturlig logaritmen för x, e-logaritmen för x	log x skall inte användas i stället för ln x, lg x, lb x eller logex, log10x, log2x.
lg x	lg x = log10x 10-logaritmen för x
lb x	lb x = log2x binära logaritmen för x 2-logaritmen för x

Trigonometriska och hyperboliska funktioner

Tecken, symbol uttryck	Betydelse	Anmärkningar och exempel
π	kvoten av en cirkels omkrets och dess diameter (utläses diame’ter)	π = 3,141 592 6…
sin x	sinus för x	(sin x)n, (cos x)n etc skrivs ofta sinnx, cosnx etc.
cos x	cosinus för x
tan x	tangens för x	tg x används fortfarande
cot x	cotangens för x	cot x = 1/tan x
sec x	secans för x	sec x = 1/cos x
csc x	cosecans för x	cosec x används också csc x = 1/sin x
Cyklometriska funktioner
arcsin x	arcus sinus för x	y = arcsin x sin y, -π/2 ≤ y ≤ π/2 Funktionen arcsin är den inversa funktionen till sin men den ovan nämnda begränsningen.
arccos x	arcus cosinus för x	y = arccos x x = cos y, 0 ≤ y ≤ π Funktionen arccos är den inversa funktionen till cos men den ovan nämnda begränsningen.
arctan x	arcus tangens för x	arctg x används fortfarande. y = arctan x x = tan y, -π/2 < y < π/2 Funktionen arctan är den inversa funktionen till tan med den ovan nämnda begränsningen.
arccot x	arcus cotangens för x	y = arccot x x = cot y, 0 < y < π Funktionen arccot är den inversa funktionen till cot med den ovan nämnda begränsningan.
arcsec x	arcus secans för x	y = arcsec x x = sec y, 0 ≤ y ≤ π Funktionen arcsec är den inversa funktionen till sec med den ovan nämnda begränsningan.
arccosec x	arcus cosecans för x	arccosec x används också. y = arccsc x x = csc y, -π/2 ≤ y ≤ π/2
Beteckningarna sin-1x, cos-1x etc för de inversa trigonometriska funktionerna skall inte användas, eftersom de kan misstolkas som (sin x)-1, (cos x)-1 etc.
Hyperboliska funktioner
sinh x	sinus hyperbolicus för x	sh x används också.
cosh x	cosinus hyperbolicus för x	ch x används också.
tanh x	tangens hyperbolicus för x	th x används också.
coth x	cotangens hyperbolicus för x	coth x = 1/tanh x
sech x	secans hyperbolicus för x	sech x 1/cosh x.
csch x	cosecans hyperbolicus för x	cosech x används också. csch x 1/sinh x.
Area funktioner
arsinh x	area sinus hyperbolicus för x	arsh x och argsh x används också. y = arsinh x x = sinh y Funktionen arsinh är den inversa funktionen till sinh.
arcosh x	area cosinus hyperbolicus för x	arch x och argch x används också. y = arcosh x x = cosh y, y ≥ 0 Funktionen arcosh är den inversa funktionen till cosh med den ovan nämnda begränsningen.
artanh x	area tangens hyperbolicus för x	arth x och argth x används också. y = artanh x x = tanh y Funktionen artanh är den inversa funktionen till tanh.
arcoth x	area cotangens hyperbolicus för x	argcoth x används också. y = arcoth x x = coth y, y ≠ 0 Funktionen arcoth är den inversa funktionen till coth med den ovan nämnda begränsningen.
arsech x	area secans hyperbolicus för x	y = arsech x x = sech y, y ≥ 0 Funktionen arsech är den inversa funktionen till sech med den ovan nämnda begränsningen.
arcsch x	area cosecans hyperbolicus för x	arcosech x används också. y = arcsc x x = csch y, y ≠ 0 Funktionen arcsch är den inversa funktionen till csch med den ovan nämnda begränsningen.
arsinh, arcosh etc kallas area sinus hyperbolicus, area cosinus hyperbolicus osv. eftersom argumentet för sinus hyperbolicus, cosinus hyperboicus osv är en area. Beteckningarna sinh-1x, cosh-1x etc för de inversa hyperboliska funktionerna skall inte användas eftersom de kan misstolkas som (sinh x)-1, (cosh x)-1 etc.

Index
Istället för att använda olika bokstäver kan bokstav med index användas:
        t. ex. a₁, a₂, a₃ … ;   x₁, x₂, x₃ … ;   A_i, A_j, A_k … ;