| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
Determinant
|
Matris |
Determinantteorins främsta uppgift är att ge lösningen till linjära ekvationssystem.
Determinant, (latin: avgränsande, bestämmande) är ett talvärde som tillordnas en kvadratisk matris enligt vissa regler. Som beteckning används två lodräta linjer på ömse sidor om schemat. Värdet av den tvåradiga determinanten (determinant av andra ordningen):
medan
En determinant av n:te ordningen:
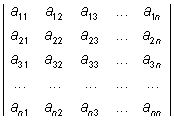
innehåller n rader och n kolumner i ett kvadratisk schema. Den har värdet Σ±a1h·a2i·a3j· … ·anm summeras över alla permutationer av de n index 1 … n. Varje term innehåller alltså en faktor från var och en av de n kolumnerna och är försedd med tecken + eller - beroende på om antalet inversioner i dess indexföljd är jämt eller udda. Determinanter innehåller alltså n!=1·2·3 … n termer.
Determinanten av 3:e ordningen innehåller 6 termer, som man erhåller genom att skriva om de två första kolumnerna efter determinanter och multiplicera och sätta till tecken som pilarna anger:
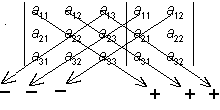
Med underdeterminanter till ett element i en determinant menar man den determinant av närmast lägre ordning, som man får genom att i den ursprungliga determinanten styrka den rad och den kolumn, i vilken elementen står och förse den med tecknet + eller - beroende på om summan av radens och spaltens nummer är jämn eller udda.
T.ex. Underdeterminanten till elementet a23 i determinanten 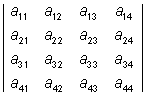 är:
är:
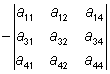 eftersom
eftersom
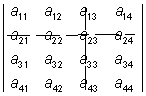
En determinant kan utvecklas efter underdeterminanterna till en rad eller en kolumn.
T.ex.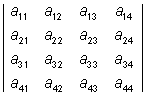 = a11 ·
= a11 · 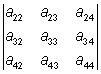 - a12 ·
- a12 · 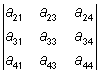 + a13 ·
+ a13 · 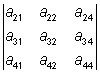 - a14 ·
- a14 · 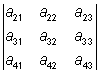
eller 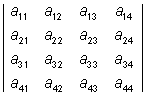 = a13 ·
= a13 · 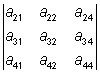 - a23 ·
- a23 · 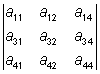 + a33 ·
+ a33 · 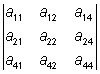 - a43 ·
- a43 · 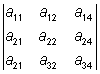
Räkneregler:
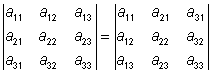
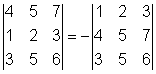
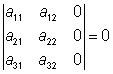
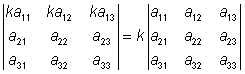
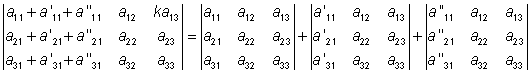
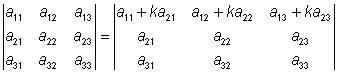
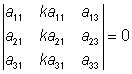
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |