| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| Aritmetik Ekvation |
Algebra
(Räkning med bokstäver) |
Online Algebra Calculator "Maxima" (gratis symbolhanterande programvara) |
Algebra är det slags matematik, där man räknar med godtyckligt givna värden, som uttrycks med bokstäver.
Bokstäverna betecknar alltså vissa värden, och
i en räkneuppgift har samma bokstav alltid samma värde.
Algebran är den del av finita matematiken som studerar sådana förhållanden, vilka uppkommer, när ett ändligt
antal räkneoperationer, s.k. algebraiska operationer utföras på en ändlig mängd utav tal. Den sysslar med ändliga processer, till skillnad från de oändliga processer som förekommer i den matematiska analysen. Beteckningen ‘abstrakt algebra‘ används ofta om algebrans mer avancerade områden till skillnad från den ‘vanliga algebran‘.
finit (lat:) = begränsad, bestämd
Som algebran handlar om obestämda tal eller kvantiteter, som kunna äga vad värde som helst, måste hon begagna allmänna karaktärer för deras beteckning. Hon betecknar därför sina kvantiteter med bokstäver i (lilla) alfabetet, emedan dessa lämna värdet obestämd och kunna betraktas som allmänna talrepresentanter.
Obekanta eller variabla storheter utmärkas vanligen genom de sista (x, y, z), bekanta eller konstanta storheter åter genom de första bokstäverna (a, b, c etc.) i alfabetet.
algebra (av arab al-djabr) matematiskt begrepp, i traditionell mening en generalisering av aritmetiken, varvid man vanligen använder bokstäver som symboler för talen (bokstavsräkning). Till algebriska symboler hör också tecken för räkneoperationer och relationer (+, -, =, >, < osv.). Med hjälp av det algebriska formelspråket kan man bl. a. uttrycka generella matematiska förhållanden. Speciellt har den traditionella algebran behandlat ekvationslösning. I allmännare mening innebär algebra även studiet av abstrakta system eller strukturer, där elementen inte nödvändigtvis är vanliga tal eller räkneoperationerna de vanliga för tal.
Algebraiska operationer
I den vanliga algebran operationerna addition, subtraktion,
multiplikation, division, rotutdragning och upphöjandet till heltals- eller rationell potens.
Icke-algebraiska eller transcendenta operationer kan exemplifieras av logaritmbildning, vars definition beror på gränsprocesser i analysen.
Algebraiskt uttryck, uttryck som är uppbyggd av ett begränsat antal algebraiska räkneoperationer. (addition, subtraktion, multiplikation, division, rotutdragning och upphöjandet till heltals- eller rationell potens.)
Koefficient i algebran, den numeriska (och konstanta) faktorn i en term.
T.ex. i 2x är koefficienten 2, i -3x²y är den -3.
Vanligen inräknas i koefficienten konstanta bokstavsfaktorer, t.ex. i 3ax² är koefficienten 3a (om a är en konstant).
Addition av algebraiska uttryck
Vid addition av algebraiska uttryck kan termer av samma slag sättas samman genom att man adderar deras koefficienter;
T.ex. (3x²-2xy+3)+(y²+3xy-5) reduceras till 3x²+xy+y²-2.
Polynom
Ett polynom (som flertermsuttryck) är allmänt ett matematiskt uttryck som kan skrivas som summan av ett antal termer.
Ett uttryckt som består av endast en term kallas monom, av två termer binom, av tre termer trinom och av flera termer polynom.
T.ex. 3ax är monom, 2x + ay² är binom och a + b - c är trinom
Vanligen är polynom, en algebraisk summa är ett helt rationellt uttryck. Vars termer består i sin tur av produkten av en koefficient (ofta en konstant) och variabler (eller bokstavsfaktorer) upphöjda till icke-negativa heltal.
Ett polynom av n:te graden i x (obestämda eller variabel, eng. polynomial) är ett uttryck på formena0 xn + a1 xn-1 + a2 xn-2 + … + an-1 x + an (n är ett naturligt tal, a0 ≠ 0 och termerna ordnas efter fallande grad.)
Polynom (med den obestämda x) och polynomfunktion betecknas vanligen med p(x).
T.ex. p(x) = x³ + 4x² - 3x + 2
Graden av ett polynom är exponenten i högsta gradstermen.
T.ex. är polynomet 3x² + 2x - 5 av andra graden.
Grad inom algebran är graden av en term x upphöjt till n det tal som anges av exponenten n. Termen x5 är således av femte graden, termerna x2y4 och 2xy2z3 är båda av sjätte graden (summan av exponenterna).
Homogent polynom
Ett polynom där alla termer har samma grad kallas homogent.
Exempelvis är polynomet 3x²y - 2xy² + y³ homogent av grad tre.
Faktorisera
Ett polynom kan ibland skrivas som en produkt med användning av den distributiva lagen. Detta kallas att uppdela i faktorer (upplösa i faktorer) eller att faktorisera. Man säger även att man bryter ut en faktor.
T.ex. 2x² + x ![]() x(2x + 1)
x(2x + 1)
Man kan även faktorisera tal. T.ex. 6 = 3 · 2 = ![]()
Utveckla (Expandera)
Motsatsen till faktorisera är expandera eller utveckla. (omforma
uttrycket så att det blir summan av termer)
T.ex. (x + y) ² ![]() x² + 2xy + y²
x² + 2xy + y²
Likformiga (likartade) termer
Flera termer kallas likformiga, om de innehåller samma bokstavsuttryck, dvs. om de antingen är identiska eller skiljer sig endast genom sifferkoefficienterna. En algebraisk summa av likformiga termer kan reduceras till en enda term.
T. ex.: 2ab + 3b² + 4ab + b² = 6ab + 4b²
Produkten av två polynomer är lika med summan av alla partiella produkter som fås, då varje term i multiplikanden multipliceras med varje term i multiplikatorn.
T. ex.: (a + b)(c + d) = (a + b)·c + (a + b)·d = ac + ad + bc + bd
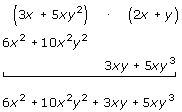
Polynomdivision (En flertermsuttryck dividerad med ett annat flertermsuttryck)
Då nu divisionen är motsats till multiplikation så måste, dividenden vara lika med summan av alla de partiella produkter som fås, då divisorn multipliceras med varje term i kvoten.
Ordna termerna i divisorn och dividenden efter exponenterna för samma bokstav;
dividera därefter dividendens första term med divisorns första term, så erhålls kvotens första term;
multiplicera hela divisorn med denna första term i kvoten, och subtrahera produkten från dividenden.
Dividera åter första termen i resten, med första termen i divisorn o. s. v.
Fortsätt detta så långt sig göra låter.
t.ex.:![]()
Divisionsalgoritmen för polynom är analog med motsvarande algoritmen för heltal, kvoten kallas för kvotpolynom, resten för restpolynom.
t.ex.: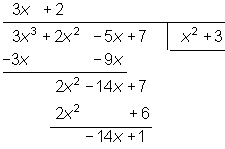
De flesta moderna symbolhanterande program kan utföra polynomdivision
t.ex. Maxima: ![]()
Ett rationellt uttryck (eller brutet rationellt uttryck) är kvoten mellan två polynom, eller ett algebraiskt uttryck som kan omformas till en sådan kvot.
t.ex. är ![]() ett rationellt uttryck, på grund av att det kan omformas till
ett rationellt uttryck, på grund av att det kan omformas till ![]() .
.
(se rationella tal)
Ett helt rationellt uttryck (vanligen kallas till polynom) är en algebraisk summa (eller det som kan omformas till en summa) vars termer består i sin tur av produkten av en koefficient (ofta en konstant) och variabler (eller bokstavsfaktorer) upphöjda till icke-negativa heltal. (polynom eller monom).
Ett irrationellt uttryck är ett uttryck som ej är rationellt.
t.ex. ![]() .
.
Algebrans fundamentalsats
Varje polynom kan skrivas som en produkt av polynom som alla är av första eller andra graden.
(med annat formulering: Varje algebraisk ekvation har minst en rot.)
T.ex. ![]()
De flesta moderna symbolhanterande program kan utföra polynomfaktorisering
t.ex. Maple: 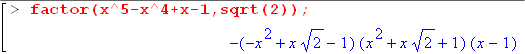
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |