WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

Kvadratrot

Kvadratroten ur ett givet tal är ett tal, vars kvadrat är det givna talet.
(En kvadratrot till ett tal a, är ett tal b, sådant att b² = a)

"Kvadratroten ur a" tecknas √a, som även utläses "roten ur a"
Sqrt(a) används i de flesta matematikprogram i stället √a.

T.ex.: √81 = 9,   √4 = 2

Kvadratroten ur ett tal är alltid positiv. Man kan inte dra kvadratroten ur ett negativt tal.

Genom definition har man dock fastslagit, att √-1 = i, där i kallas den imaginära enheten.

Härav följer t.ex.	√-2 = i√2
	√-3 = i√3
	√-4 = i√4 = 2i
	=

Kubikrot

Kubikroten ur (eller tredje roten ur) ett givet tal är ett tal, vars kub är det givna talet
(En kubikrot till a är ett tal b, sådant att b³ = a.)

"Tredje roten ur a" tecknas ³√a, som även utläses "kubikroten ur a"

T.ex.: ³√125 = 5,   ³√-27

n:te rot

n:te roten ur ett givet tal är ett tal, vars n:te potens är det givna talet.
(En n:te rot till a är ett tal b, sådant att bⁿ = a).

"n:te roten ur a" tecknas som ⁿ√a eller som potens a^1/n.

Rotutdragning

Den räkning genom vilken roten till en kvantitet söks, kallas rotutdragning eller evolution, och är fullkomlig motsats till upphöjning.

= a

Tecknet √ kallas rottecken eller rotmärke, a kallas radikanden, b kallas roten och n kallas rotexponenten eller rotindexet.

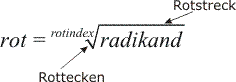
Rot inom matematiken en allmän beteckning för lösning till en ekvation, speciellt lösningen till ekvationen x ⁿ = a.

Om rötter

• Jämte reella rötter

  Varje positivt tal har exakt två reella n:te rötter, om n är jämnt; den positiva av dessa skrivs ⁿ√a (är n = 2, skriver man i allmänhet √a.

  Exempel: ⁴√16 = 2  (ytterligare en reell rot finns; den skrivs -⁴√16 = -2).

  Ett negativt tal har ingen reell n:te rot, om n är jämnt, ty varje jämn potens av ett godtyckligt reellt tal är alltid icke-negativ.

  Exempel: ²√-8 existerar ej som reellt tal.

• Udda reela rot

  Är n udda, existerar exakt en reell n:te rot till talet a (positivt eller negativt); denna skrivs ⁿ√a och har samma tecken som a. Det gäller (ⁿ√a)ⁿ = a.

  Exemplar: ³√-8 = -2; ³√8 = 2.

• Komplexa rötter

  Tillåts komplexa tal som rötter, gäller följande generella resultat:
  Varje (komplext) tal har exakt n (komplexa) n:te rötter.

  Exemplar:
  De två kvadratrötterna till -1 är i och -i, och
  de tre kubikrötterna till 8 är 2, -1 + i√3 och -1 - i√3.

Rotlagar

     n och k är naturliga tal och större eller lika med 2.

Multiplikation:	n√a·n√b = n√a·b
Division:
Upphöjning:	om a > 0
Rotutdragning:
Logaritm:

T.ex.:
√25 = 5, eftersom 0 < 5 och 5² = 25
(-5)² = 25, men √25 ≠  -5,
√a² = |a|

Rötter av tal kan också skrivas som potenser:
t.ex.: ³√8 = 8^1/3 och ³√a² = a^2/3