WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

Komplext tal

Komplext tal är tal av allmännare slag än de reella talen och som tillåter räkning med rötter ur negativa tal.

Om b ≠ 0 kallas a + ib ett icke-reellt tal t. ex. 2 + 3i.
Om dessutom a = 0 kallas talet ett rent imaginärt tal. t. ex. 3i

En polynomfunktion kan sakna reella nollställen, men har alltid ett komplext nollställe. Denna viktiga egenskap motiverar utvidgningen från de reella talen, , till de komplexa, . Talet i är ett av nollställena till polynomet z² + 1 (man väljer godtyckligt ett; det andra blir då - i). Det anmärkningsvärda är att när man har infört detta nollställe i, så får också alla andra polynom nollställen, nämligen lika många som gradtalet.

Den imaginära enheten i elektrotekniken betecknas med j.

Talplan

Varje komplext tal kan åskådliggöras som en punkt i ett tvådimensionellt koordinatsystem, det komplexa talplanet som också brukar kallas det Gausska talplanet eller Argand diagram.

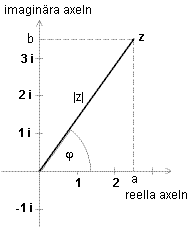Talet z representeras av en punkt med koordinaterna a och b. Avståndet från talpunkten till origo representerar talets absolutbelopp eller modyl eller talvärde av |z|. För detta gäller eller generellt Positiva vinkeln φ mellan ovannämnda sträcka och den reella axeln kallas argumentet för z, φ = arg(z) och som framgår av figuren gäller

Polära formen

Varje komplext tal (z = a + ib) kan skrivas i polär form:

där r är absolutbelopp, ett icke negativt reelt tal (r = |z|)
och φ är argument, ett reellt tal, (φ = arg(z)).

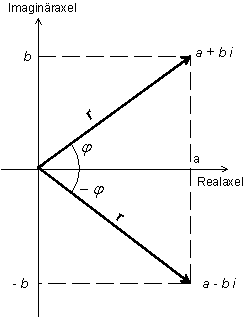
Konjugat

Talet  = a - ib kallas det konjugerade komplexa talet (även kallat konjugatet) till z = a + ib. Det gäller att || = |z|, arg () = - arg (z)   och z·= a² + b² = |z|²

Räkna med komplexa tal

Man kan räkna med komplexa tal på samma sätt som med reella tal om man ersätter i² med -1.

Potenser av i kan alltid reduceras till ±1 eller ± i; till exempel är i³ = i²·i = (-1)·i = -i   och   i⁴ = i²·i² = (-1)·(-1) = 1.

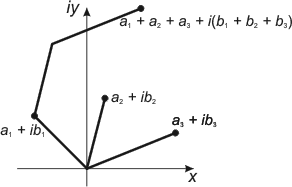
Vid addition och subtraktion av komplexa tal skall talens realdelar, resp. imaginärdelar adderas (subtraheras) var för sig (a + ib) + (c + id) = (a + c) + i(b + d) En addition av komplexa tal representeras grafiskt av ett polygontåg.

Komplexa tal multipliceras på följande sätt:

(a + ib)(c + id) = ac + iad + ibc + i²bd  = (ac - bd) + i(ad + bc).

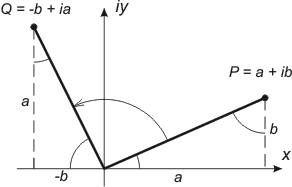
För en godtycklig punkt P = a + ib får vi att (a + ib)·i = ai + i²b = -b + ia Multiplikation av ett komplext tal med den imaginära enheten i kan tolkas som en rotation 90º mot visarna på ett ur.

Komplexa tal divideras genom att man multiplicerar täljare och nämnare med det konjugerade komplexa talet till den senare, varigenom nämnaren blir ett reellt tal:

Om man uttrycker de komplexa talen i polär form r(cos φ + i·sin φ), fås följande formler för multiplikation och division:

respektive

Detta innebär att vid multiplikation multiplicerar man absolutbeloppen och adderar argumenten, och vid division dividerar man absolutbeloppen och subtraherar argumenten.

de Moivres formel

Potenser av komplexa tal i polär form erhålls genom formeln

  på exponentiell form

De Moivres formel gäller för exponenter som är bråk lika väl som för heltal, men i det förra fallet är inte värdet entydigt bestämt.

Exempel: z = 3 + 7 i

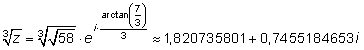
Sammanhanget mellan trigonometriska, hyperboliska, exponential- och logaritmfunktioner i det komplexa

Exponentialfunktion

, , ,

Funktionen e^z är periodisk enligt 2πi: e^z = e^z+2kπi (om k är heltal), t.ex. e⁰ = e^2kπi = 1, e^{(2k + 1)πi} = -1.

e^ix = cos x + i sin x;       Eulers formler


e^x = cosh x + sinh x;

Principialvärde

Låt z vara ett komplext tal:

z = x + iy = re^iφ

      (exponentialfunktionen har perioden 2π)

ln z = ln r + iφ + 2nπ i (logaritmen är en oändligt mångtydig funktion, vars grenar skilja sig från varandra med multipler av 2π i). Då n = 0, fås principialvärdet.

Ekvationer med komplexa koefficienter

Två komplexa tal a + ib och c + id är lika om och endast om a = c och b = d, dvs om och endast om real- och imaginärdelarna är lika.

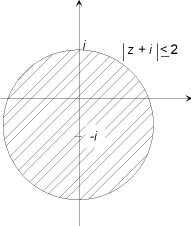
Exemplar för relationer som beskriver vissa delar av det komplexa planet:

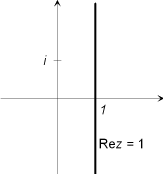
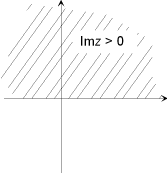
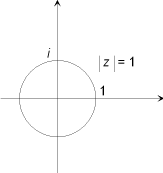
Lös ekvationen

x⁴ = 16 i

Skriv båda led i polarform!

För likhet erfordras att talens absolutbelopp och argument var för sig är lika. Alltså gäller

r⁴ = 16
r  = 2

och vidare (eftersom perioden för sinus och cosinus är 360º)

4 φ = 90º + n·360°     n = 0, ±1, ±2, …

  φ = 22,5º + n·90°

Den sökta roten är alltså

(Den första roten x₁ erhålles för n = 0, den andra n = 1 etc)

Lös ekvationen

2(x + y) + i(y + 1) = 6 + 9i

Talens realdelar måste vara lika

2(x + y) = 6

och talens imaginärdelar vara lika

y + 1 = 9

Ekvationens lösning är alltså

x = -5   och   y = 8

En tvåpolens impedans är Z = (475 + j 219) Ω
Tvåpolens admittans är