WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

Trigonometri

Trigonometri är det område av matematiken i vilket sambanden mellan en triangels olika storheter (vinklar och sidor) beskrivs med trigonometriska funktioner.

Trigonometriska funktioner (Cirkelfunktioner)

Trigonometriska funktioner är sammanfattande benämning på de matematiska funktionerna:

Med traditionellt skrivsätt använder man inga parenteser efter sin, cos, tan e.t.c. förkortningar om de är produkter eller potenser:
sin ωt = sin (ωt)  däremot  y·sin x = (sin x)·y
sin²x = (sin x)·(sin x)   och   sin x² = sin (x·x)

Definitioner och grundbegrepp

Trigonometriska relationer för spetsiga vinklar

De triginometriska funktionerna kan för spetsiga vinklar (< 90º)  definieras som förhållandena mellan vissa sidor i en rätvinklig triangel. (den oberoende variabeln är en vinkel mellan 0 och 90º)

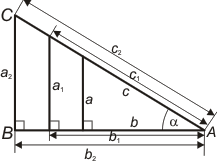Sambanden mellan de trigonometriska funktionerna för vinkeln α :

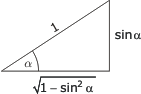
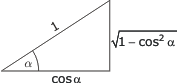
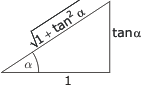
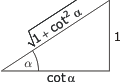
Eftersom α och β är komplementvinklar (α + β = 90°)
sin β = sin (90° - α) = cos α	cos β = cos (90° - α) = sin α
tan β = tan (90° - α) = cot α	cot β = cot (90° - α) = tan α

Trigonometriska funktioner definierade med hjälp av enhetscirkeln

Enhetscirkeln är en cirkel med radie 1 (en längdenhet).

1 = enhet = OC = OE x = vinkeln i bågmått = bågen AC sin x = BC cos x = OB tan x = AD cot x = EF sec x = OD csc x = OF

Trigonometriska funktioner för godtyckliga vinklar

För att definiera trigonometriska funktionerna för godtyckliga vinklar använder man en enhetscirkel med centrum i origo i ett ortonormierat koordinatsystem. (Den har ekvationen x² + y² = 1.)
Vinkeln α mellan x-axeln och en rörlig radie betraktas. (För α > 0 görs därvid vridningen i positiv riktning, för α < 0 görs vridningen i negativ riktning.) Då är sinus resp. cosinus för vinkeln lika med y- resp x-koordinaten för den rörliga radiens ändpunkt. Radiens förlängning skär de vertikala och horisontella tangenterna och ger tan α   resp. cot α.

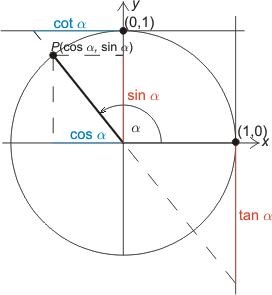För punkten P gäller sinus sin α = y-koordinaten för P cosinus cos α = x-koordinaten för P tangens tan α =     cos α ≠ 0 cotangens cot α =     sin α ≠ 0 Funktionsvärdet ändras ej om till vinkeln läggas en multipel av ett varv (360º), varför de trigonometriska funktionerna är periodiska med perioden = ett varv. Vid övergång från vinkelmått (grader) till bågmått (radianer) ersätts vinkeln α av längden av den mot α svarande bågen x, med r = 1. Om α = 360º (helt varv), så är x = 2 π (cirkelns omkrets). Alltså är 1º = 2π/360 = π/180 = 0,01745 radianer och 1 radian = 180º/π = 57,3º Funktionerna y = sin x och y = cos x är alltså definierade för alla x, medan för y = tan x och y = cot x vissa värden måste uteslutas. De trigonometriska funktionerna kunna utvecklas i potensserier, där vinkeln, x är uttryckt i bågmått.

Periodicitet

Vilket innebär att för alla heltal k (k )

Sin x, tan x och cot x är udda funktioner medan cos x är jämn.

En funktion f sägs vara udda om f(-x)=-f(x) för alla x i definitionsområdet och jämn om f(-x)=f(x) för alla x i definitionsområdet.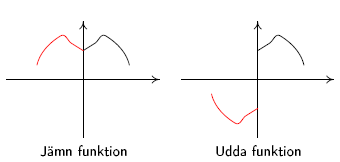

Grafer av trigonometriska funktioner

De trigonometriska funktionerna återges grafiskt med vinkeln som abskissa och funktionsvärdena som ordinata. Som vinkelenhet används radianer.

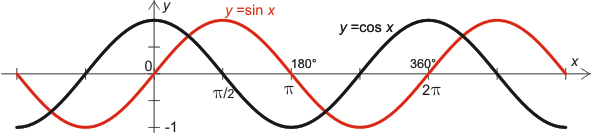
Cosinuskurvan erhålles genom att sinuskurvan parallellförskjuts π/2 åt vänster. Detta följer av relationen
sin (x + ) = cos x

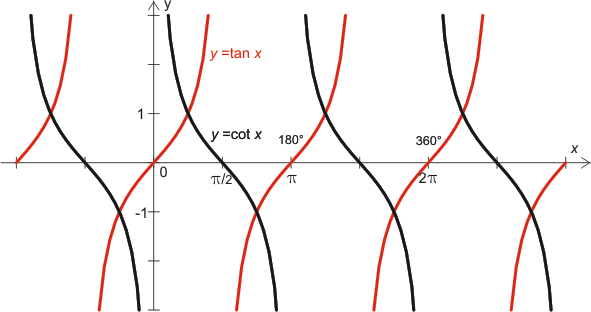
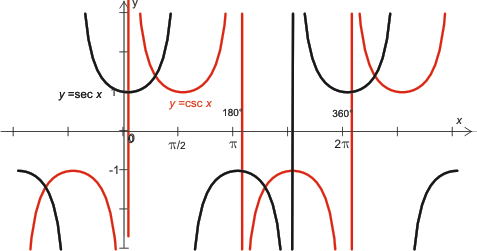
De trigonometriska funktionernas värden (och gränsvärden) för vissa vinklar

α grader 0° 30° 45° 60° 90° 120° 180° 270° x radianer 0 π sin 0 1 0 -1 cos 1 0 - -1 0 tan 0 1 ± ∞ - 0 ± ∞ cot ∞ 1 0 - ∞ 0

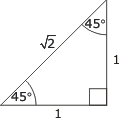
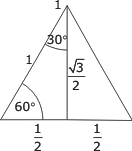1/√2 ≈ 0,707     1/√3 ≈ 0,588     √3 ≈ 1,732     √3/2 ≈ 0,866

Trigonometriska identiteter

Likheterna gäller för alla värden på x:

Samband mellan trigonometriska funktioner

  (sin x)² skrivs vanligen sin²x

	sin2 x	cos2 x	tan2 x	cot2 x
sin2 x =		1-cos2x
cos2 x =	1-sin2x
tan2 x =

Trigonometriska funktioner med tan x/2

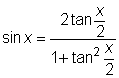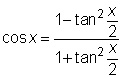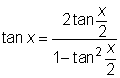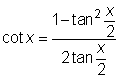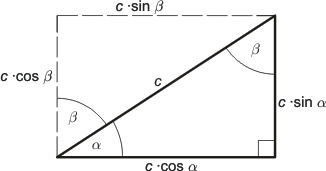
Trigonometriska funktioner av summor och skillnader:

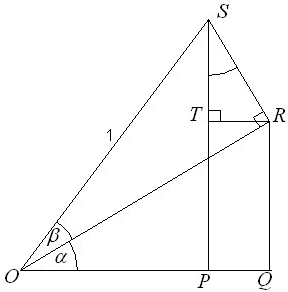om OS = 1 då RS = sin β och OR = cos β eftersom ΔRST ~ ΔROQ RST α ST = cos α · sin β     RT = sin α · sin β RQ = sin α · cos β PT RQ = sin α · cos β sin (α + β) = PT + ST = sin α · cos β + cos α · sin β   cos (α + β) = OQ - PQ = cos α · cos β - sin α · sin β eftersom OQ = cos α · cos β och PQ RT = sin α · sin β

sin(x ± y) = sin x cos y ± cos x sin y		cos(x ± y) = cos x cos y  sin x sin y
sin 2x = 2 sin x cos x		cos 2x = cos2 x - sin2 x cos 2x = 2 cos2 x - 1 cos 2x = 1 - 2 sin2 x
tan 2x =
sin 3x = 3 sin x - 4 sin3 x		cos 3x = 4 cos3 x - 3 cos x

Trigonometriska produktformler:

Trigonometriska summaformler: