Triangelsolvering - Formelsamling - Matematik minimum - Terminologi och begreppsförklaring

Matematik minimum - Terminologi
En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik
A B C D E F G H I J K L M N O P Q R S T U V X Y Z Å Ä Ö
Klicka på någon av bokstäverna

Nedladdning

Triangelsolvering
Formler för beräkning av trianglarnas obekanta element

- trianglar
- beräkning av rätvinkliga trianglar
- beräkning av snedvinkliga trianglar
- trigonometriska funktioner

Beteckningar

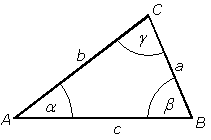Triangels hörn betecknas vanligen med A, B, C (i motsols) och själva triangel betecknas med ΔABC.
Motsvarande vinklar till hörn betecknas med grekiska bokstäver: α , β och γ.
Motstående sidor till hörn betecknas med små bokstäver: a, b och c. (sidan a står mot vinkeln α , etc)
s är halva omkretsen av triangeln, dvs :

Sinussatsen

I en triangel är sinus för vinkeln proportionell mot längden av de motstående sidorna.

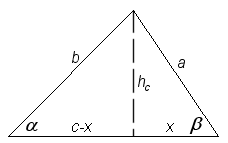
Bevis:
h_c = a sin β
h_c = b sin α
a sin β = b sin α

Cosinussatsen

I varje triangel är kvadraten på en sida lika med summan av kvadraterna på de båda andra sidorna minus dubbla produkten av dessa sidor och cosinus för mellanliggande vinkel.

a² = b² + c² - 2bc · cos α
b² = a² + c² - 2ac · cos β
c² = a² + b² - 2ab · cos γ

Bevis:
(c - x)² + h_c² = b²
x² + h_c² = a²
(c - x)² - x² = b² - a²
b² =c² + a² - 2cx

eftersom x = a·cos β
då b² = c² + a² - 2ac·cos β

Tangenssatsen

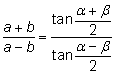(Det finns två analoga formler)

Vinklar

Halvvinklar

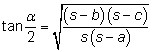Längder

Höjdens längd Längden av en höjd i en triangel är: Det finns två analoga formler för h_b och h_c
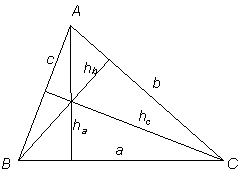Medians längd Längden av en median i en triangel är (Det finns två analoga formler för m_b och m_c)
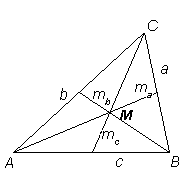Bisektris' längd Längden av en bisektris i en triangel är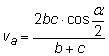 Det finns två analoga formler för v_b och v_c
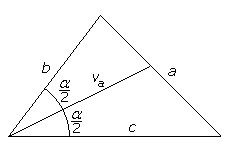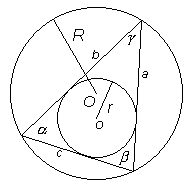
Cirklar Radien till den omskrivna cirkeln: Radien till den inskrivna cirkeln: