| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
|
Punkt Linje Geometrisk ort Area och omkrets |
Plan Figur Kropp |
Geometri
Grundbegrepp
|
Storhet (Kvantitet) Geometriska storheter Analytisk geometri Rymdgeometri |
Den delen av matematiken som handlar om storheter (kvantiteter), vilka har utsträckning (dimension) heter geometri.
Geometri den gren av matematiken som sysslar med rumsbegrepp som punkt, linje och plan samt med de figurer och kroppar som bildas med hjälp av dessa.
Den första kända geometrin uppstod i det gamla Egypten ur behovet att kunna bestämma arealer. Den var likaledes nödvändig inom den dåtida högt utvecklade byggnadskonsten.
En mer vetenskaplig form fick geometrin genom alexandrinen Euklides,
vars verk Stoicheia (lat Elementa) rymmer en logisk tankebyggnad som stått sig till våra dagar. På 1600-talet skapade Descartes den analytiska geometrin genom att införa koordinatsystem för beskrivningen av geometriska figurer och kroppar.
Den beskrivande geometrin, införd år 1800 av fransmannen Gaspard Monge (1746-1818), anger metoder
för att beskriva kroppar genom projicering av dem på två eller tre plan. Något senare (1822) grundade fransmannen
Jean Victor Poncelet (1788-1867) den projektiva geometrin, som avser perspektivistisk projektion samt lagarna
för densamma.
(Ur FOCUS 2000 © Norstedts)
Punkt
Punkten är en odefinierad storhet (kvantitet) som representerar ett objekt med läge utan utsträckning (dimension).I datagrafiken och i skolmatematiken kallas de geometriska figurerna (linjer, cirklar, plan, sfärer, etc.)
för geometriska objekt. De uppfattas att vara sammansättning av punkter och även definieras som: "punktmäng i noll, en eller flera dimensioner" (t.ex. i boken Matematiktermer för skolan).
Däremot i den riktiga (euklidiska) geometrin en-, två- och tredimensionella figurer består inte "dimensionslösa" punkter. Punkterna är yttersta ändarna av en linje, som linjer är det yttersta av en yta och ytor är yttersta av en kropp.
Punkten har inga delar.
Två räta linjer kan inte skära varandra i mer än en punkt.
Punkterna betecknas vanligen med stora, kursiva bokstäver: A, B, C, … P.
Ofta angives en punkt med tillhjälp av ett kors (×). Punkten läge markeras då av skärningspunkten.
A = B säger att punkten A har samma läge som punkten B (A sammanfaller B), eftersom punkterna saknar storhetsvärde.
I planet bestämmer två olika punkter en rät linje,
dvs. genom två givna punkter går exakt en rät linje.
Tre olika punkter i planet, vilka ej ligger på en rät
linje, bestämmer entydigt en cirkel eller en triangel.
 |
 |
 |
Tre olika punkter i rummet, vilka ej ligger på en rät linje, bestämmer entydigt ett plan.
I ett koordinatsystem i planet representeras en punkt av ett par av tal, koordinater (x, y).
Kurva
En kurva är en endimensionell figur, (en längd utan bredd,) som kan vara rak (rät) eller krökt, obegränsad eller begränsad av en eller två ändpunkter.
Begreppet kurva omfattar sträcka och rät linje.
Den matematiska terminologin skiljer sig här från vardagligt och tekniskt språkbruk. En kurva förknippas ofta med något som är krökt, som t ex i vägkurva, och linje med något som är smalt men inte nödvändigtvis rakt, som t ex i kraftlinje. Om man speciellt vill påpeka en linjes egenskap att inte vara krökt, talar man ibland om en rät linje.
En kurva i planet (plan kurva) är en kurva som helt ligger i ett plan; den framställs ofta som grafen för en ekvation av formen y = ƒ(x) eller F(x,y) = 0 i koordinaterna x och y.
Algebraiska kurvor (deras ekvationer bildade med hjälp av algebraiska operationer)
x² + y² = 4 är ekvationen för en cirkel med radien 2 och medelpunkten i origo,
y = 2x + 6 är ekvationen för den räta linjen genom punkterna (0,6) och (-3,0).
Transcendenta kurvor framställs av transcendenta funktioner, t ex y = sin x.
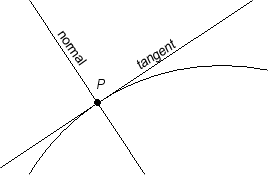
Tangenten till kurvan i en punkt
Tangenten är en rät linje som har en punkt gemensam med en kurva så att kurvans riktning i skärningspunkten (tangeringspunkten) sammanfaller med den räta linjens riktning.
I planet är normalen till en kurva i en punkt P på kurvan är den räta linje som är vinkelrät mot tangenten till kurvan i punkten P.
En normal till en sträcka genom dennas mittpunkt kallas mittpunktsnormal (mittnormal) till sträckan.
 |
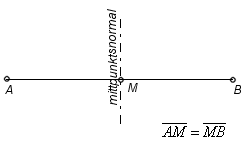 |
Linje
En linje är en kurva som är rak (rät) och obegränsad åt båda håll.
Om en linje icke är rät, kallas den krokig.
Kroklinje är ett gemensamt namn för alla övriga linjer som icke är räta.
Om en linje består av två eller flera räta linjer, som inte ligger i rät linje med varandra, kallas linje bruten, numera kallas öppen polygon.
Om en punkt P ligger på en rät linje k säger vi att linjen k går genom P.
Genom två punkter A och B går en enda rät linje, vilket betecknas "linjen AB".
Om två olika linjer l och m i planet har en punkt P gemensam, sägs l och m skära varandra i P, som kallas skärningspunkt (intersektion).|
|

|
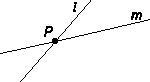
|
Halvlinje, stråle
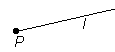
En halvlinje är en del av en linje som åt ena hållet är begränsad av en ändpunkt och åt andra hållet är obegränsad. Utgå räta linjer från en gemensam punkt i olika riktningar, kallas dessa linjer strålar.
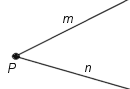
En vinkel bildas av två strålar, som utgår från samma punkt.
Sträcka, avstånd
| En sträcka är en del av en linje som begränsas av två ändpunkter. En sträcka med ändpunkterna A och B kan betecknas sträckan AB. Återstoden av linjen kallas sträckan AB:s förlängning. En båge (en begränsad del av en krokig linje) kan icke alltid föras längs efter den krokiga linjen, så att den till hela sin längd faller efter linjen. |
Sträckor och andra tillräckligt enkla kurvor har längd.
Avståndet mellan två punkter A och B är längden av sträckan AB.
En rät linje är det kortaste avståndet mellan två punkter.
Längden av sträckan AB kan betecknas |AB| eller (AB) eller ![]() vilket utläses "längden av AB".
vilket utläses "längden av AB".
Längden av en godtycklig kurva bestäms genom att man bestämmer ett antal punkter på denna och ritar en (öppen) polygon genom dessa punkter. Sedan bestämmer man längden av denna polygon.
Parallell
Parallella är de räta linjer, som är aldrig kunna skära varandra, utan överallt behåller samma avstånd sinsemellan, om dem än oändligen utdragas. Ordet parallell betyder jämlöpande. Två kroklinjer sägs vara parallella, om i varje punkt normalen till den ena kroklinjen är normal till den andra och det mellan båda kroklinjerna liggande stycket är konstant. Parallellaxiom är den 5. postulat i Euklides' Elementa, som kan formuleras så att till varje rät linje finns exakt en parallell rät linje genom varje punkt (utanför den ursprungliga linjen), vilket matematikerna inte upplevde som lika naturligt som de andra axiomen i Euklides geometri. |
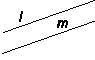 |
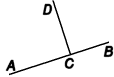
Normal, vinkelrät (perpendikulär) linje, perpendikel
|
En rät linje (CD) sägs vara vinkelrät (perpendikulära) mot en annan, då linjen med den andra formerar lika stora vinklar (ACD och BCD) på båda sidor om sig. Beteckning: En normal eller en perpendikel är en rät linje som är vinkelrät mot en annan rät linje. Den riktning eller linje som en tråd, varvid någon fritt nedhängande tyngd är fästade, kallas en vertikal, lodrät riktning eller linje. Den linje som är vinkelrät mot en vertikal-linje kallas för en vågrät eller horisontal linje. |
 |
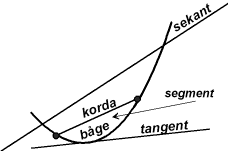
Segment
|
Ett segment är yta som begränsas av en kurva och en rät linje (korda). Segment är i allmänhet varje begränsad del av en rät linje (sträcka) eller kurva (båge), ibland också en begränsad del av en plan eller buktig yta. En båge är en del av en kurva som ligger mellan två punkter på kurvan. En korda är en sträcka som förenar två punkter på en kurva eller yta. En sekant är en rät linje som skär en kurva i två eller flera punkter. |
 |
Yta
En yta är en kontinuerlig (sammanhängande) tvådimensionell del av rummet. Den har ingen tjocklek. Den kan ha olika form och den kan t ex vara buktig eller plan samt begränsad eller obegränsad.Plan
Ett plan är en yta som är obegränsad åt alla håll och inte är buktig.
En plan är bestämt av ettdera av följande villkor:
(1) tre punkter P, Q och R som ej ligger på en rät linje skall tillhöra planet;
(2) en linje l och en punkt P, som ej ligger på l, skall tillhöra planet;
(3) två varandra skärande räta linjer skall tillhöra planet;
(4) två parallella, icke sammanfallande räta linjer skall tillhöra planet.
Två olika plan i rummet skär varandra längs en rät linje eller också skär de varandra inte alls; de kallas då parallella.
Planimetri (plan geometri)
Studiet av geometriska figurer i planet; vanligen de elementära aspekterna på linjer, vinklar, trianglar, fyrsidingar, polygoner och cirklar.
Figur
En plan figur (plan form) är en yta, begränsad av en eller flera linjer (kurvor).
Kroppen (solid figur) är ett begränsat rymdområde
Kropp (geometrisk kropp, solid figur)
En (geometrisk) kropp är den del av rymden, som begränsas av en helt sluten yta. (Kroppen är ett begränsat rymdområde.)
En kropp har alltså tre dimensioner: längd, höjd och bredd. Ytan är kroppens gräns.
Med kropp menas i fysiken också föremål i allmänhet, viss mängd materia.
Geometrisk ort
Geometrisk ort (locus) är sammanfattningen av alla de punkter, som uppfyller ett visst villkor.
(Numera används begreppet punktmängd istället.)
T.ex. Cirkeln är den geometriska orten för alla punkter som har samma avstånd till en given punkt.
|
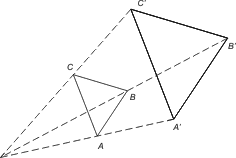
Likformighet Likformiga är två geometriska rätliniga figurationer (figurer, kroppar), om motsvarande vinklar överensstämmer och motsvarande sträckor alltid bildar samma förhållande. Begreppet kan med vissa modifikationer utsträckas till krokliniga figurer eller kroppar, helt eller delvis begränsade av buktiga ytor.
Likformighet beteckans med ~ symbol. ΔABC ~ ΔA1B1C1 Likställighet Om föreningslinjerna mellan motsvarande punkter i två figurer går genom samma punkt och motsvarande sträckor och "strålar" har konstant förhållande, sägs figurerna vara likställda. |
 |
Kongruens
Två figurer (eller geometriska konfigurationer t.ex. vinklar) är kongruenta, om de efter förflyttning, vridning (ev. förenad med vändning) kan bringas att fullständigt täcka varandra.
Kongruens betecknas ofta med ![]() symbol.
symbol.
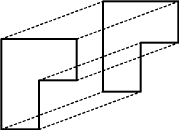
Parallelförflyttning (parallellförskjutning,) eller translation |
 |
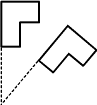
| Vridning kring en punkt (även kallad rotation) Alla punkter vrids lika mycket kring den fixa punkten. |
 |
Symmetri
En figur i planet eller i rummet är symmetrisk med avseende på punkten O, symmetripunkten eller medelpunkten, om varje korda genom O halveras av O. Ellipsen i planet och ellipsoiden i rummet har sådan punktsymmetri. En figur uppvisar spegelsymmetri i en rät linje eller i ett plan om alla kordor, vinkelräta mot linjen eller planet, halveras av denna symmetrilinje resp. detta symmetriplan. Om alla kordor i en fast riktning halveras, och riktningen inte är vinkelrät mot symmetrilinjen eller symmetriplanet, talar man om sned symmetri.
a. Axelsymmetri: en plan figur är symmetrisk kring en axel, om den är spegelbilden av sig själv i axeln.
Ex. En kvadrat är symmetrisk kring diagonalerna och kring mittpunkts normalerna. En liksidig triangel är symmetrisk kring höjderna. En cirkel är symmetrisk kring en diameter och en ellips kring storaxeln eller lillaxeln.
b. Strålsymmetri: en regelbunden polygon kan genom vridning kring tyngdpunkten (symmetricentrum) fås att täcka sig själv. Den vinkel figuren ska vridas är 360º/n, där n är antalet sidor i figuren. En liksidig triangel täcker
sig själv genom vridning 360º/3=120º kring centrum av den omskrivna cirkeln.
c. Punktsymmetri: en plan figur sägs vara symmetrisk kring en punkt, om den efter vridning 180º täcker sig själv.
Ex. En parallellogram är symmetrisk med hänsyn till diagonalernas skärningspunkt.
Projektion
Projektionen är inom matematiken avbildning av visst slag. I geometrisk bemärkelse innebär projektion avbildning av en figur (punkt, kurva eller kropp) på en rät linje eller ett plan med hjälp av räta linjer, projektionsstrålar. Vid parallellprojektion är strålarna parallella, vid centralprojektion går de alla genom en och samma punkt (projektionscentrum).
Vanligen avser man rätvinklig projektion.
Som en generalisering av den geometriska betydelsen finns också en algebraisk betydelse av projektion. Denna avser en linjär avbildning av ett vektorrum på ett delrum (projektionens bildrum) som flyttar varje punkt parallellt med ett visst annat delrum (projektionens nollrum), vilket innebär att avbildningen är linjär och att varje punkt i bildrummet projiceras på sig själv (dvs. man får inget nytt om man upprepar projektionen två gånger).
Konstruktioner
Geometriska konstruktioner är strängt taget endast sådana konstruktioner, som kan utföras med hjälp av (ograderad) linjal och passare.
Exempel: 1. Att dela given sträcka vinkelrät mitt itu
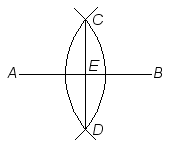 |
Givet är: en begränsad rät linje eller en sträcka Sökes: en rät linje, som är vinkelrät mot den givna sträckan och går genom dess mittpunkt. Konstruktion: Tag sträckans ändpunkter A och B till medelpunkter för cirklar med lika stora radier - som måste vara större än halva den givna sträckans längd. Dessa cirklar skär varandra i två punkter, C och D. Sammanbind dessa punkter medelst en rät linje, CD. Denna linje, CD, är vinkelrät mot den givna sträckan AB och skär denna mitt itu i en punkt, E. |
Exempel: 2. Att i och kring en cirkel in- och omskriva en reguljär (regelbunden) femhörning.
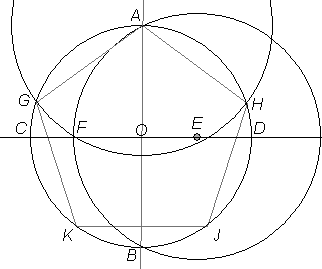
|
Drag i cirkeln två mot varandra vinkelräta diametrar, AB och CD. Dela den ena diameterns ena hälft, OD, mitt itu i E, Tag E till medelpunkt för en genom A (och B) gående cirkel, som skär samma diameter CD i en punkt F, så är AF längden av den inskrivna femhörningens sida.
Fullborda denna femhörning, AGKJH.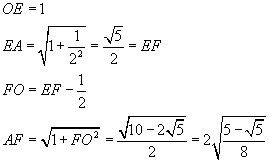
|
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |