| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| Grafen till en funktion Grafiska lösningar |
Grafer - Grafiska lösningar |
Ekvation Funktion Geometri |
Graf
Graf (diagram) är en bild (en grafisk framställning) som åskådliggör sambandet mellan två eller flera storheter (variabler).Ekvationens graf
Med en lösning av en ekvation med två obekanta (x och y) menar vi en ordnat par (a, b) som satistifierar ekvationen när vi ersätter x med a och y med b. Om vi markerar alla ordnade par i lösningsmängden i ett rätvinkligt koordinatsystem, får vi en kurva som vi kallar ekvationens graf.
T.ex.:
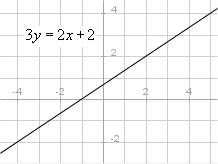
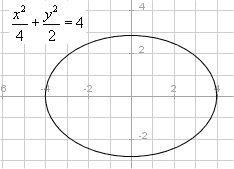
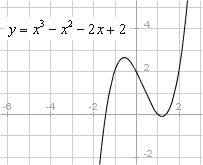
Grafen till en funktion
Man kan erhålla en geometrisk bild av en funktion y = ƒ(x) om man inför två mot varandra vinkelräta tallinjer, s. k. axlar, med gemensamt origo och låter punkterna på den ena axeln, x-axeln, motsvara värdena av den oberoende variabeln x och punkterna på den andra axeln, y-axeln, motsvara värdena av den beroende variabeln y. Mot två genom y = ƒ(x) sammanhörande värden x, y svarar en punkt i planet med koordinaterna x, y i förhållande till det rätvinkliga axelsystemet. Sammanfattningen av alla sådana punkter utgör en geometrisk bild av funktionen y = ƒ(x).
T.ex.:
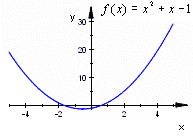
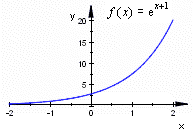
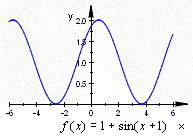
Definitioner som gäller i den svenska skolan:"En reell funktion (av en variabel) är en funktion ƒ för vilken såväl Df som Vf är delmängder av
.
När x uppfattas som en punkt på talaxeln, kallas ƒ(x) funktionsvärdet i punkten x.
Mot mängden av paren (x, ƒ(x), svarar en punktmängd i planet som kallas funktionens graf, och som i många fall är en kurva, kallad funktionskurva." (Matematikterminologi i skolan 1979 SÖ)
Förstagradsekvationer
Ex. Lös ekvationen 3x + 4 = 0
Man sätter 3x + 4 lika med t. ex. y och ritar i ett koordinatsystem in den räta linje, som har ekvationen y = 3x + 4
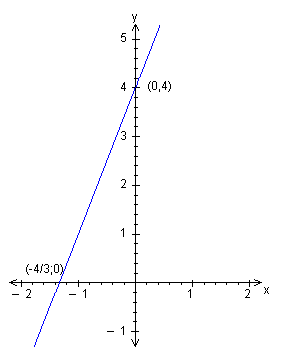 |
Två punkter är tillräcklig för att bestämma en rät linje. Man ser på fig. att linjen skär y-axeln i (0,4) och x-axeln i (- y (och därmed den givna ekvationen) antar värdet 0 för x = - x = - |
Två förstagradsekvationer med två obekanta (Ekvationssystem)
Ex. Lös ekvationerna
y = -2x + 4 y = 3x De två ekvationer framställer varsin rät linje. Dessa två linjer inritas i ett koordinatsystem, och koordinaterna för deras skärningspunkt avläses. Koordinaterna för skärningspunkten är rot till ekvationerna.
På figuren avläses koordinaterna till (1, 2).
x = 1 och y = 2 är roten till de båda ekvationerna.(ekvivalenta ekvationer) framställer samma linje, det finns alltså oändliga många gemensamma punkter.
Identiska ekvationer y = -2x + 4 2y = -4x + 8 framställer parallella linjer, som inte har någon punkt gemensamt.
Motstridande ekvationer y = -2x + 4 y = -2x+ 8
Andragradsekvationer
Rötterna till ekvationen ax2 + bx + c = 0 kunna grafiskt bestämmas genom uppritande av kurvan y = ax2 + bx + c och avläsande av de x-värden, för vilka y blir = 0, d.v.s. x-koordinaterna för kurvans skärningspunkter med x-axeln. Funktionskurvan kan intaga tre väsentligt olika lägen i förhållande till x-axeln.
|
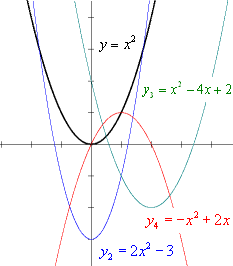 |
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |