WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

De reella talen kan åskådliggöras på en talaxel även kallad tallinje.

Mängden av reella tal kan avbildas på punkterna på en rätt linje, tallinjen.
Denna avbildning är en bijektion, varmed menas, att mot varje tal svarar precis en punkt, mot varje punkt svarar precis ett tal.

De reella talen utgör en ordnad mängd. Vi säger, att a < b (läs: a är mindre än b) om b - a > 0. På tallinjen ligger då a till vänster om b.

På tallinjen finns:

1. utgångspunkt (O, origo, begynnelsepunkt , nollpunkt)
   (origo(lat.) betyder ursprung, begynnelse)
2. enhetspunkt (E) och
3. positiv riktning, som visas med en pil.

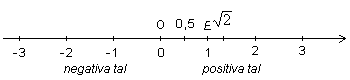
OE kallas enhetssträckan.
Med abskissan för en punkt på tallinjen förstås punktens avstånd till origo; avståndet räknas med sitt vederbörliga (+ eller -) tecken.

På linjen i positiv riktning från O ligger alla positiva tal.

De negativa talen ligger på linjen i negativ riktning från O.
På tallinjen ovan är talen -1, +0,5 och inritade.

På tallinjen ligger de negativa talen på ena sidan (vanligen den vänstra) och positiva talen på den andra sida.

Inverterade talet:

Två storheter sägs ha reciproka (inverterade) värden om produkten av dem är lika med 1.

Så är t.ex. talen 11/4 och 4/11 reciproka, eftersom (11/4)·(4/11)=1.

Om produkten av två tal är 1, sägs vardera talet vara inverterade talet till det andra talet.

Inverterade talet till 2/3 är 3/2.