WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

I modern matematik ett allmännare begrepp än funktion.
Orden funktion, operator och transformation används delvis synonymt med ordet avbildning.

En avbildning ƒ av en mängd X (kallas definitionsmäng eller domän) in i en mängd Y (kallas målmängd eller kodomän) är en tillordning av precis ett element i Y till varje element i X.
Den matematiska beteckningen för detta är ƒ: X  Y.
Det till elementet x tillordnade elementet i Y kallas bilden av x och betecknas ƒ(x), och avbildningen ƒ anges även med x  ƒ(x). Avbildningen är given om varje par (x, y) med y = ƒ(x) är givet.
Avbildningens definitionsmängd (D_f) är X, dess bildmängd eller värdemängd (V_f) är mängden av alla ƒ(x), vilket är en delmängd av Y.

En avbildning kallas
- injektiv om olika punkter i X har olika bilder (x₁≠ x₂   ƒ(x₁) ≠ ƒ(x₂)),
- surjektiv om dess bildmängd är hela Y (V_f = Y), och
- bijektiv om den är både injektiv och surjektiv.

En bijektion har alltid en invers, som betecknas ƒ^-1. Det gäller att D_ƒ^-1 = Y och V_ƒ^-1 = X, samt att (ƒ^-1 ƒ)(x) = x för alla x  X och (ƒ ƒ^-1)(y) = y för alla y  Y.

Exempelvis är avbildningen: (där är mängden av de reella talen)

ƒ: →, x  x2	varken injektiv eller surjektiv	(ƒ(2) = ƒ(-2) = 4; talen 2 och -2 har samma kvadrat) (det finns inget reellt tal med x2 = -1)
g: →, x  x3	bijektiv	(till varje reellt tal y finns precis ett tal x sådant att x3 = y, nämligen kubikroten ur y)

Relation: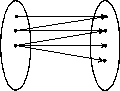

Funktion: (moderna uppfattning)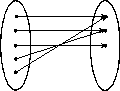

Bijektiv avbildning: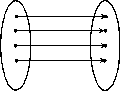

ƒ:a  b betyder att ƒ(a)=b, där a och b tillhör specificerade mängder

Relation i matematiken samband mellan två storheter. Relation i en mängd är ett samband mellan elementen i mängden.

Vissa relationer i matematiken uttrycks med speciella symboler, t ex likhet, '='; ordning '≤'; kongruens ''; likformighet '~'.