| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| Noll Oändlighet Algebraiska och transcendenta tal Bråktal Reella tal Talsystem |
Tal - Talsystem |
Bråk, bråkuttryck Komplext tal Mängd Storhet Storhetsvärde |
Tal
Tal är ett matematiskt grundbegrepp, symbol eller (siffer-)tecken för (obenämnd, abstrakt) matematisk storhet som används vid räkning. Tal anger förhållandet mellan storheter och värden, d.v.s. hur många gånger större är storheten än enheten. Ett tal anger hur många saker och ting finns i ett mängd.
Antal
Om man vid en mängd av saker (en mängd) bortser från de enskilda sakernas olika egenskaper och endast håller kvar vad som är oberoende av dessa skiljaktigheter, erhålles begreppet antal, genom vilken den givna mängden skiljer sig från en sådan med flera eller färre föremål av samma slag som den givnas.
När man med talet förenar enhetens namn, t. ex. tre skålpund, åtta kronor, o.s.v., så kallas detta ett benämnt tal; de abstrakta talen kallas i motsats därtill obenämnda.
Ett som enhet
Talet 1 (ett) är en abstrakt, obenämnd storhet, betyder endast "det finns", "det existerar" eller "vi antar att det existerar", "det är sig själv", "det är helt", "det är fullständigt". Därför har inga betydelser multiplicering, dividering och upphöjande med 1.Noll
Talet 0 (noll) är abstrakt storhet som finns för att ange att ingenting finns. Noll betyder att "det finns inte", "det existerar inte". Noll används markering för begynnelse punkt, utgångsläge och för att ange det finns ingen skillnad mellan värdena, det finns inget avstånd mellan punkterna. Dividera med noll är en självmotsägelse eftersom inget kan delas med inga antal lika stora delar.Oändlighet
Oändlighet är en mer filosofiskt än matematiskt begrepp. Man kallar en linje oändligt om linje kan godtyckligt förlängas.Talindelningar
Algebraiska tal - Transcendenta tal
Algebraiska och transcendenta tal
Algebraiska tal är sådana tal, som kunna vara rötter till algebraiska ekvationer med heltalskoefficienter, (det är nollställe till ett polynom ![]() med rationella koefficienter, där a0 ≠ 0).
med rationella koefficienter, där a0 ≠ 0).
Exempel: √2 är rot till x² - 2 = 0
![]() (gyllene kovten,
(gyllene kovten, ![]() ) är rot till x² - x - 1 = 0.
) är rot till x² - x - 1 = 0.
i (imaginära enheten) är rot till x² + 1 = 0.
1 + √2 är rot till x² - 2x - 1 = 0.
Transcendenta tal kunna icke vara rötter till algebraiska ekvationer med heltalskoefficienter.
Exempel: e, π
Reella tal:
Reella tal anger storhetsvärde av de verkliga och de abstrakta storheterna samt anger räknebara storhetsförhållanden. T.ex. Abel plockade tre gånger fler blommor än Bertil.
Varje reellt tal hör en punkt på tallinjen.
Mängden av reella talan betecknas med ![]() ; x
är reellt tal betecknas med: x
; x
är reellt tal betecknas med: x ![]()
![]()
![]() Icke-reellt tal är ett komplext tal (
Icke-reellt tal är ett komplext tal (![]() ), vars imaginärdel inte är lika med 0.
), vars imaginärdel inte är lika med 0.
![]()
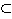
![]()
![]()
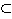
![]()
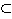
![]()
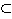
![]()
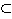
![]()
Ordningslagar för de reella talen
Vi använder beteckningen a < b (utläses: a mindre än b) och den likbetydande b > a (utläses: b större än a).
< och > kallas för olikhetstecken.Om a och b är reella tal, gäller en och endast en av relationerna
a < b, a = b, b < a
För godtyckliga reella tal gäller:
a < b och b < c medför, att a < c (transitivitet av relationen "<"),
a < b medför, att a + c < b + c,
a < b och c > 0 medför, att ac < bc (en olikhet får multipliceras med ett positivt tal),
om x < y är reella tal, finns ett rationellt tal r, så att x < r < y,
om a och b är givna positiva tal, finns ett naturligt tal n, så att a < n·b (den arkimediska egenskapen).
Man säger, att mängden av de reella talen är ordnad.
Positivt tal
Ett tal är positiv om det är större än noll.
Negativt tal
Ett tal är negativt om det är mindre än noll.
Negativa tal anger storhetsvärde de storheterna som vid summering minskar summan. T.ex. motriktad förflyttning, avdrag.
Till varje positivt tal a finns ett motsvarande negativt tal -a.
En storhet betraktas negativt om man addera storheten till en annan storhat och resulatat blir mindre än storheten som adderas till.
T.ex. B är negativt om C < A i A + B = C
Motsatta tal
Ett positivt tal och motsvarande negativa tal kallas motsatta.
Det motsatta talet kallas även den additiva inversen.
Det motsatta talet till 0 är 0. Talet 0 är varken positiv eller negativ.
Rationella tal:
Rationella tal (eller kommensurabla tal = mätbara tal) kallas sådana tal, som har möjlighet att exakt mätas med enheten. Hit hör således de hela talen (bland dem även noll innefattad) och bråk(tal), vilkas täljare och nämnare är eller har möjlighet att reduceras till hela tal.
Talmängden av rationella tal (betecknas med ![]() ) består av alla hela tal och alla bråktal, som kan uttryckas i formen p/q där p och q är hela tal, q ≠ 0.
) består av alla hela tal och alla bråktal, som kan uttryckas i formen p/q där p och q är hela tal, q ≠ 0.
![]()
Decimaltal (tal i decimalform med ändlig antal siffror t.ex. 0,5 och 1,225) och oändliga decimalbråk med periodiska decimaltalutväckling (t.ex. 1,312 = 1,312312312...) är rationella tal.
Icke-rationellt tal är ett irrationellt tal.
Hela tal:
Tal, som uppkommer genom upprepade sammanläggningar av en odelad enhet, kallas hela tal (av Euklides).
Mängden av alla positiva och negativa heltal och 0 betecknas med: ![]() ={… , -3, -2, -1, 0, 1, 2, 3, …}
={… , -3, -2, -1, 0, 1, 2, 3, …}
Naturliga tal, eller hela positiva tal:
Naturliga tal anger storhetsvärde av storheter som består av enheter som vanligen naturligt skiljer sig från varandra eller deras storlek motsvarar multipel av enheter. T.ex. tre dinosaurusar, fem träd men 5 kilo mjöl.
Mängden av naturliga tal är
![]() = {1, 2, 3, 4, …}
Det finns matematiker som kallar även 0 för naturligt tal.
= {1, 2, 3, 4, …}
Det finns matematiker som kallar även 0 för naturligt tal.
Mängden av hela positiva tal är: ![]() + = {1, 2, 3, 4, …}
+ = {1, 2, 3, 4, …}
Induktionsaxiomet: Om för A 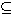
![]() + gäller
+ gäller
1. 1 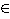 A 2. För all p
A 2. För all p 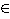
![]() + : p
+ : p 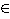 A
A 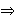 p + 1
p + 1 ![]() A
A
så är A = ![]() +
+
Jämna tal:
Heltal som är (jämnt) delbara med 2: … -4, -2, 0, 2, 4, 6, 8, …
Udda tal:
Heltal som inte är delbara med 2: … -3, -1, 1, 3, 5, 7, …
Konsekutiva tal:
Tal, som omedelbart följer varandra i talföljd. Vanligen de är naturliga tal: T.ex. 57, 58.
Figurtal, figurligatal eller figurativa tal
(av lat. numeri figurali), sådana talserier, som bildas genom successiv addition av termerna i aritmetiska serier eller i andra figurtalserier. Så bildas t.ex. ur den aritmetiska serien
1, 2, 3, 4, 5, 6, 7 … genom successiv addition figurtalserien
1, 3, 6, 10, 15, 21, 28 …, … (triangulärtal)
och ur denna på samma sätt en ny serie av figurtal
1, 4, 10, 20, 35, 56, 84 … (pyramidaltal)
och 1, 8, 27, 64, 125 … (kubiktal = tredje potens av ett naturligt tal).
| Polygonaltal Polygonaltal av 1:a ordningen kallas triangeltal (triangulärtal): 1, 3, 6, 10, 15, 21, 28 o.s.v. Polygonaltal av 2:a ordningen kallas kvadrattal: 1, 4, 9, 16, … (andra potens av ett naturligt tal) Polygonaltal av 3:a ordningen kallas pentagonaltal: 1, 5, 12, 22, … Polygonaltal av 4:a ordningen kallas hexagonaltal. Den allmänna formeln för polygonaltal av p-te ordningen är: |
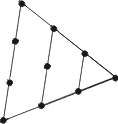 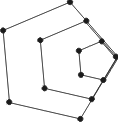 |
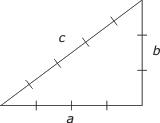
Pythagoreisk trippel Naturliga tal a, b och c sådana att a² + b² = c² En rätvinklig triangel med sidorna a, b, c upfyller enligt Pythagoras sats denna ekvation. |
 |
Bråktal (se sidan om bråk)
Rationella tal som är icke heltal kallas för bråk (bråktal).
Bråkuttryck
Bråk är ett uttryck av formen ![]() ,
a kallas täljare, b nämnare. Strecket kallas bråkstreck.
,
a kallas täljare, b nämnare. Strecket kallas bråkstreck.
Decimaltal
Ett rationellt tal, som med ett ändligt antal siffror kan skrivas i decimalform, kallas ett decimaltal.
Ett avslutat decimalbråk (ändligt decimalbråk) kan skrivas som allmänt bråk genom att man skriver decimalerna som täljare och som nämnare en etta följd av lika många nollor som antalet decimaler. Bråket förkortas som möjligt.
Exempel:![]()
Avgörande för om ett tal är decimaltal är om det går att skriva i decimalform, med ändligt antal siffror, och inte om är skrivet i denna form. (![]() som kan skrivas 3,5 är decimaltal men
som kan skrivas 3,5 är decimaltal men ![]() som inte kan skrivas med ett ändligt antal siffror i decimalform är inte ett decimaltal)
som inte kan skrivas med ett ändligt antal siffror i decimalform är inte ett decimaltal)
Irrationella tal
De icke-periodiska, oändliga decimalbråken kallas irrationella (icke rationella) tal eller inkommensurabla tal. Exempelvis är det reella talet 0.12112111211112111112…Algebraiska irrationella tal (![]() )
)
Transcendenta irrationella tal (![]() )
)
Imaginära tal
Imaginärt tal anger storhetsvärde av skenbara (vanligen magasinerade, vridna eller tidsförskjutna) storheter som självmultiplicerad resulterar minskning av en reell storhet.
t.ex. ett tal som
multiplicerat med sig själv ger en negativ produkt.
( ![]() , se komplext tal)
, se komplext tal)
Talsystem (talbeteckningssytem)
är ett system för att beteckna och benämna i första hand heltalen. Ett talsystem bör dels vara sådant att många tal kan framställas med ett fåtal tecken (siffror), dels vara lämpat för aritmetiska operationer.
Positionssystem är ett talbeteckningssystem i vilket ett teckens (en siffras) betydelse beror av dess plats (position) i talbeteckningen.
Varje plats (position) har ett bestämt platsvärde som en heltalspotens av systemets bas.
I 340 står "trean" på en plats med platsvärdet 100 och betecknar talet 300.
Talet 375,125 kan med hjälp av platsvärdena skrivas
375,125 = 3·100 + 7·10 + 5·1 + 1·0,1 + 2·0,01 + 5·0,001
Detta brukar kallas utvecklad form.
Ett positionssystem definieras av en bas och behöver siffror, inkl. 0, som till antalet är lika med basen.
I decimaltalsystemet, även kallat tiosystemet är basen 10 och siffrorna 0 till 9, med s.k. arabiska siffror: 0, 1, 2, 3, 4, 5, 6, 7, 8 och 9.
De infördes i Europa på 1300-talet och är de mest använda i världen. Moderna araber använder siffror som ser annorlunda ut: ![]()
Ett tal skrivet i decimalsystemet sägs vara skrivet i decimalform.
 |
|
Siffersumman (eller tvärsumman) av ett tal är den summa som erhålles, när talets siffror adderas.
Siffersumman av 235 är 2 + 3 + 5 = 10
Ett binärt talsystem (dyadiskt talsystem) har två som bas och behöver bara två tecken, 1 och 0.
Positionsvärdet multipliceras här med två för varje steg åt vänster. Så t ex är det binära talet 1 011 uttryckt i det decimala systemet detsamma som 1·8+0·4+1·2+1·1=11. Det binära systemet har kommit till användning särskilt inom datatekniken, där alternativen 1 och 0 kan motsvaras av två olika tillstånd hos en elektronisk krets eller ett magnetiskt medium. I mikrodatorer används ofta det hexadecimala talsystemet med 16 som bas. Talen betecknas med siffrorna 0-9 samt bokstäverna A-F, där A står för talet 10 och F för talet 15.
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |