| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
Kombinatorik |
Kombinatorik kallas den del av aritmetiken, som sysslar med att undersöka, på hur många sätt ett givet antal element kan ordnas och sammanställas i grupper.
Man skiljer på permutationer, kombinationer och variationer (delpermutationer).
| Alla element (n) ingår i sammanställningen | Permutationer | Pn = n! | |
| En del av elementen (k eller r) ingår i sammanställningen (k < n) |
Olika ordningsföljd räknas för samma sammanstälningar Kombinationer av k st valda bland n st utan hänsyn till ordning. |
Kombinationer | nCr = |
| Olika ordningsföljd räknas för olika sammanställningar Permutationer av k st valda bland n st med hänsyn till ordning. |
Variationer delpermutationer |
nPr = |
|
Permutationer
En permutation är en sammanställning av n element. Varje element förekommer en och endast en gång i permutationen.
A. Permutationer utan upprepning. Alla element är olika.
Antalet permutationer är då n! (n-fakultet)
| Pn = n! |
| abc | bac | cab |
| acb | bca | cba |
Ex. 7 elever kan ställas upp i rad på:
P8 = 7! = 1·2·3·4·5·6·7 = 5040 olika sätt.
B. Permutationer med upprepning. Alla n element är inte olika.
Det är t.ex. två grupper, den första med k1 lika element, den andra med k2 lika element.
Antalet permutationer blir då:
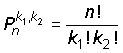 |
Ex. Elementen A, A, A, B och B permuteras.
Antalet permutationer är:
![]()
AAABB AABAB AABBA ABAAB ABABA ABBAA BAAAB BAABA BABAA BBAAA
n!=1·2·3·…·(n - 1)·n
T.ex. är 5!=1·2·3·4·5=120.
Definition med en rekursionsformel:n! = n·(n - 1)!
Om man nämligen väljer n = 1 blir ju uttrycket 1! = 1·0! och för att det ska stämma måste 0! vara 1.
Betecknas även med Π (n)
Gamma-funktion utvidgar fakultetsbegreppet till alla positiva reella tal:
![]()
![]()
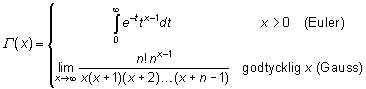
Kombinationer
En kombination är en sammanställning av endast k av n olika element (k < n). Olika ordningsföljder har inte någon betydelse. Så t.ex. är ab och ba samma kombination
A. Kombinationer utan upprepning. Varje element får förekomma endast en gång
Antalet kombinationer är (binomialformeln):
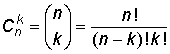 |
Betecknas även: C(n,k); Cn,k; nCk (nCr).
Binomialkoefficienten ![]() (utläses "n över k" eller "n välj k") är koefficienten av xn i utvecklingen av
(1 + x)n och kan enligt binomialsatsen beräknas som
(utläses "n över k" eller "n välj k") är koefficienten av xn i utvecklingen av
(1 + x)n och kan enligt binomialsatsen beräknas som
![]()
Ex. Antal kombinationer med 5 element till en mängd
med 8 element:
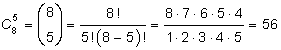
B. Kombinationer med upprepning. Ett element får förekomma flera gånger i kombinationen.
Antalet kombinationer är:
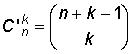 |
Ex. Två av de fyra elementen a, b, c, och d kombineras.
Antalet kombinationer är:
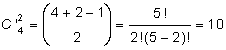
Kombinationerna är: aa ab ac ad bb bc bd cc cd dd
Variationer (delpermutationer)
En variation är en sammanställning av bara k av n olika element (k < n).
Olika ordningsföljder räknas som olika sammanställningar.
Antalet permutationer av p olika objekt valda bland n givna
A. Variation utan upprepning. Om ett element får endast användes en gång är antalet variationer:
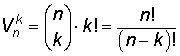 |
Betecknas även: P(n,k), nPk (nPr)
Ex. Två valda av de tre elementen 1,2 och 3 permuteras.
Antalet variationer är:
![]()
12 13 21 23 31 32
B. Variation med upprepning. Samma element får användas flera gånger.
Antalet variationer är:
Ex. Två av de tre bokstäverna A, B och C varieras.
Antalet variationer är:
![]()
AA AB AC BA BB BC CA CB CC
Binomialsatsen
Newtons binomialteorem.
Utvecklingen ![]()
där n är ett positivt heltal.
![]()
Koefficienterna kallas binomialkoefficienter och ![]() .
.
Om n inte är ett positivt heltal gäller i stället den oändliga serieutvecklingen: ![]()
Binomialkoefficienterna kan ställas upp i den s.k. Pascals triangel, som bygger på det viktiga sambandet ![]()
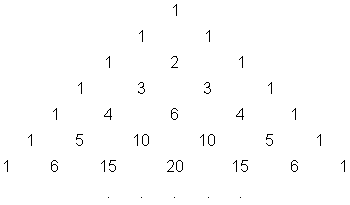
så att t.ex.![]()
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |