| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| Största gemensamma divisorn Minsta gemensamma dividenden |
Delbarhet - Multipel - Prefix
|
Aritmetik Division Multiplikation |
Delbarhet
Ett tal som utan rest kan dela ett annat (d.v.s. som ger ett helt tal till kvot), sägs vara delare till (divisor till) detta tal.
Ett tal a är delbart med ett tal b om kvoten a/b är ett heltal.
| Man säger då även att | "b är delare till a" |
| eller att | "b går upp i a" |
| eller att | "b går jämnt upp i a" |
| eller att | "a är en multipel av b" |
Delbarhetsregler för heltal
Det hela talet n är en delare (divisor) till det hela talet N om det finns ett heltal q,
sådant att
N = q · n ;
om detta gäller sägs N vara delbart med n.
| Ett helt tal är delbart med | |
| 2, | om sista siffran (entalet) är jämt eller 0. |
| 3, | om talets siffersumma är delbar med 3. |
| 4, | om det tal, som bildas av de två sista siffrorna är delbart med 4. |
| 5, | när sista siffran är 0 eller 5. |
| 6, | när villkoren för 2 och 3 både är uppfyllda. |
| 7, | när talets tiotal minus dubbla antalet av talets ental är delbart med 7. Ex.:392 är delbart med 7 (39-4=35) |
| 8, | när det tal, som bildas av de tre sista siffrorna är delbart med 8. |
| 9, | när talets siffersumma är delbar med 9. |
| 10, | när talets sista siffra är en nolla. |
| 11, | när summan av varannan siffra i talet (siffror med udda ordningsnummer: entalen, hundratalen, tiotusentalen osv.) minus summan av de övriga siffrorna (siffror med jämn ordningsnummer) är delbar med 11. |
| 12, | när villkoren för 3 och 4 båda är uppfyllda. |
| 13, | när antalet tiotal i talen plus fyra gånger sista siffran (antalet ental)
är delbart med 13. Ex.:6409 är delbart med 13 (640+36=676 |
Resterna vid heltalsdivision
I modulär aritmetik räknar med med resterna vid division med ett heltal n.
Beteckningen a mod b betyder resten då a divideras med b.
Ex:
7 mod 5 = 2
16 mod 2 = 0
3 mod 7 = 3
-1 mod 3 = 2
- 7 mod 2 = 1
Kongruens modulo
Två hela tal a och b sägs vara kongruenta modulo m (skrivs a ≡ b mod m) om division med m ger samma rest. Exempelvis är 23 och 11 kongruenta modulo 6 eftersom både 23 och 11 ger resten 5 vid division med 6. Detta kan också uttryckas som att a - b är jämnt delbart med m, dvs. i exemplet att skillnaden 23 - 11 = 12 är jämnt delbar med 6. Om m = 2 är två tal kongruenta (modulo 2) om antingen båda är udda eller båda jämna.
Primtal
Ett naturligt tal (a > 1), som endast är delbart med sig själv (a) och enheten (1), kallas primtal.
Primtalen under 100 är: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 och 97.
Ett helt tal som inte är primtal, kallas ett sammansatt tal och det kan uppdelas i primfaktorer.
|
Faktorisering av heltal Varje (positivt) heltal kan skrivas som en produkt av primtal.(t.ex. 12 = 2 · 2 · 3)
Faktorisering med hjälp av WolframAlpha på Intrnet: factor(486612) |
|
Exemplar av primfaktorer med "Maxima" (gratis symbolhanterande programvara):(%i5) factor(486612);
(%i6) factor(486612+1);
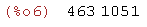
Uppdelning i primfaktorer används, när man ska bestämma minsta gemensamma multipeln och största gemensamma delaren.
Sörsta gemensamma delaren
Gemensam delare
Ett helt tal som utan rest dividerar två, eller flera hela tal, sägs vara en gemensam delare (gemensam divisor) till dessa tal.
Om t.ex. 5 är gemensam delare till 10 och 25
Tal som icke har någon gemensam delare (utom 1) kallas relativa primtal.
t.ex. 35 och 12 är relativt prima
Största gemensamma delaren (SGD) - (GCD - greatest common divisor) är den största av de gemensamma delarna.Största gemensamma delaren är produkten av gemensamma primfaktorer i den högsta potens de ingår i alla givna talen.
t.ex. GCD(100,75)=25) eftersom 100=52·22 , 75=52·3 och 25=52
Största gemensamma delaren med hjälp av WolframAlpha på Internet: gcd(100,25)
Ett naturligt tal som är lika med summan av sina delare (inklusive 1, men exklusive talet självt). De fem första perfekta talen är 6, 28, 496, 8128, 33550336.
Till exempel är 28 ett perfekt tal eftersom 28=1+2+4+7+14.
Alla positiva tal kan skrivas som kedjebråk, dvs. på följande form:
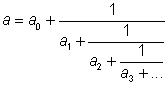
t.ex.
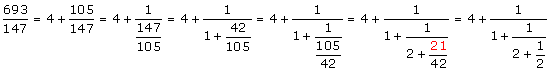
Man skriver kortare: 4;122.
Talen 4, 1, 2 och 2 kallas kedjebråkets partialnämnare. 21 är den största gemensamma delare till 693 och 147.
(%i3)
cf(693/147);
![]()
(%i4)
cfdisrep(%);
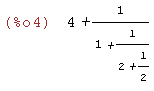
Alla rationella tal kan framställas av ett ändligt, de irrationella talen av ett oändligt kedjebråk.
t.ex.: 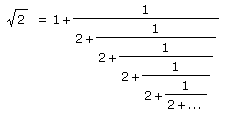
Bråket ![]() (gyllene snitt) kan, eftersom det är en rot till ekvationen
(gyllene snitt) kan, eftersom det är en rot till ekvationen ![]() skrivas:
skrivas:
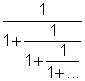
Multipel (mångdfald)
Om en given storhet (ett givet tal) mångdfäldigas (multipliceras) ett visst antal gånger, så sägs den erhållna produkten vara en mångfald (multipel) av den givna storheten (det givna talet).
Ett tal a sägs vara multipel (mångfald) av det talet b, om b är delare till a,
dvs. om det existerar ett heltal n, sådant att a = n · b.
Minsta gemensamma multipeln
Ett tal, som har den egenskapen, att det är jämt delbart med vart och ett av flera andra givna tal, kallas dessa tals gemensamma mångfald (multipel) eller gemensamma dividend.
12, 24 och är jämt delbara med såväl 4 som 6 och följaktligen är 12, 24 och 36 gemensamma dividender (multiplar) till 4 och 6.
Den minsta gemensamma multipeln (MGM) eller minsta gemensamma dividend (LCM - least common multiple)
är den minsta av de gemensamma multiplerna.
T.ex. LCM(16,12)=48
16 = 24 12 = 3 · 22 48 = 3 · 24
Minsta gemensamma multipel med hjälp av WolframAlpha på Internet: lcm(16,12)
Minsta gemensamma nämnaren
Gemensam nämnare
Till två eller flera bråk, ett heltal eller polynom som är delbart med var och en av nämnarna i de olika bråken, dvs. en gemensam multipel till nämnarna.
Till exempel har bråken ![]() den gemensamma nämnaren 30; de har också 60, 90 etc som gemensamma nämnare. De två bråken
den gemensamma nämnaren 30; de har också 60, 90 etc som gemensamma nämnare. De två bråken ![]() och
och ![]() har den gemensamma nämnaren 2(x+1)(x-1)(x-2); en annan gemensam nämnare är 2(x+1)2(x-1)(x-2). Bråk med samma nämnare kan adderas genom att man helt enkelt adderar täljarna och behåller nämnaren oförändrad.
har den gemensamma nämnaren 2(x+1)(x-1)(x-2); en annan gemensam nämnare är 2(x+1)2(x-1)(x-2). Bråk med samma nämnare kan adderas genom att man helt enkelt adderar täljarna och behåller nämnaren oförändrad.
Den minsta gemensamma nämnaren till ett antal bråk är den minsta gemensamma multipeln till deras nämnare.
| Talfaktor | Prefix | Exampel | ||
| Benämning | Beteckning | |||
| 1024 | yotta | Y | ||
| 1021 | zetta | Z | ||
| 1018 | exa | E | 1 exajoule | 1 EJ |
| 1015 | peta | P | 1 petameter | 1 Pm |
| 1012 | tera | T | 1 terajoule | 1 TJ |
| 109 | giga | G | 1 gigawatt | 1 GW |
| 106 | mega | M | 1 megavolt | 1 MV |
| 103 | kilo | k | 1 kilometer | 1 km |
| 102 | hekto | h | 1 hektogram | 1 hg |
| 101 | deka | da | 1 dekalumen | 1 dalm |
| 10-1 | deci | d | 1 decimeter | 1 dm |
| 10-2 | centi | c | 1 centimeter | 1 cm |
| 10-3 | milli | m | 1 milligram | 1 mg |
| 10-6 | mikro | μ | 1 mikrometer | 1 μm |
| 10-9 | nano | n | 1 nanohenry | 1 nH |
| 10-12 | piko | p | 1 pikofarad | 1 pF |
| 10-15 | femto | f | 1 femtometer | 1 fm |
| 10-18 | atto | a | 1 attosekund | 1 as |
| 10-21 | zepto | z | ||
| 10-24 | yokto | y | ||
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |