| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
|
Dignitet - Kvadrat - Kub Tiopotens Potenslagar |
Potens
Upphöjning
|
Rotutdragning Logaritm |
Den upphöjning, (potensupphöjning, exponentiering eller involution) är en mellan två tal definierad matematisk operation.
Potensuttryck och exponent
En potens är ett uttryck av formen an(utläses "a upphöjt till n" eller "a n").
a och n kan vara vilket tal som helst (positivt eller negativt, helt eller brutet, rationellt eller irrationellt, reellt eller imaginärt).
I potensen a n kallas a basen (eller roten), och n kallas exponenten.
Uttrycket an betecknas som a^n i de flesta matematikprogram
Dignitet
Heltalspotens (Potens med positiv heltalsexponent) eller dignitet
Produkten av n faktorer som alla är lika med a (upprepad multiplikation) betecknas a n och kallas n:te potensen (n:te digniteten) av a, och a kallas potensens (dignitetens) bas (eller rot) samt n dess exponent.
| (n är ett naturligt tal) |
Varje tal är första potensen (digniteten) av sig själv, (a = a1)
den andra potensen (digniteten) kallas kvadrat (a·a = a²),
den tredje kub (a·a·a = a³)
och den fjärde bikvadrat. (a·a·a·a = a4).
![]() eftersom
eftersom 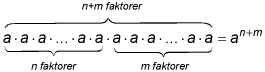
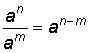 ,
, ![]() och
och ![]()

Utvidgning av dignitetsbegreppet
Exponenten är noll
| Definition: a0 = 1 om a ≠ 0. | 00 är ej definierad gränsvärdena: 00 = 1 enligt de flesta nya räknedosor, program som räknar 000 = 01 = 0 och 0000 = 00 = 1 o.s.v. |
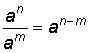 ska även gälla om m = n ska även gälla om m = n erhålles 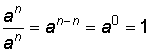 |
|
Negativ exponent
| Definition: |
|
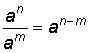 , sätter vi nu in m = 0 , sätter vi nu in m = 0 erhålles 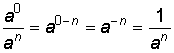 |
|
Rationell exponent (bråktalsexponent)
| Definition: |
||
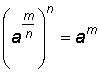 eftersom eftersom 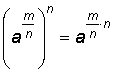 n:te rot av både sidor (enligt definition av rotutdragningen): |
||
Irrationell exponent
Definition av potensen a x, för irrationell x exponent
kräver en gränsprocess: ![]()
Imaginär exponent
För det komplexa talet z = x + iy definieras ez som
![]()
Tiopotens
En potens med basen 10 kallas tiopotens.
Platsvärdena i tiosystemet kan skrivas som tiopotenser med heltalsexponenter.
10 -2 = 0,01
10 -1 = 0,1
10 0 = 1
10 1 = 10
10 2 = 100
10 6 = 1 000 000
En million är alltså = 106. Detta utläses 6:te potensen av 10 eller 10 upphöjt till 6.
"Scientific notation" t.ex. 2,45·103 kallas grundpotensform.
Potenslagar:
| Multiplikation: | ||
| Division: | 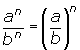 |
|
| Upphöjning: | ||
| Rotutdragning: | ||
| Logaritm: |
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |