| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
|
Logaritmlagar Logaritmsystem Räkna ut exponenten 10-logaritm (lg) Naturlig logaritm (ln) Logaritmekvationer |
Logaritm |
Aritmetik Potens - Upphöjning Rotutdragning Tal |
Logaritmen för ett tal (a) i ett visst logaritmsystem menas exponent (x), vartill systemets bas (b) skall upphöjas för att bli lika med talet a.
Med tecken uttryckt är definitionen:
Logaritmeringen är en mellan två tal definierad matematisk operation, att söka (och hitta) en exponent för en potens vars värde är det givet tal.
Exponentiering (upphöjning) och logaritmering motsatta räknesätt: exp(ln(a)) = a, lg(10b) = b
Logaritmen* är ett annat ord för gällande exponenten (med avseende på ett givet tal).
* Av grekiska orden (λογος logos) förhållande och (αριϑμος arithmos) tal, eftersom i en följd av formen 100:101:102:103:104: o.s.v. i vilken exponenterna bildar en aritmetisk följd, bildar själva termerna en geometrisk följd, eller en följd av lika stora förhållanden, och exponenterna utvisar hur långt förhållandet ligger från första termen 100.
Exemplar:
| bas: 10 |
x = log10 a | logaritm (exponent): | -2 | -1 | 0 | 1 | 2 | … | -0,92082.. | 0,07918.. | 1,07918.. | 2,07918.. | 3,07918.. |
| a = 10x | tal (antilogaritm): | 0,01 | 0,1 | 1 | 10 | 100 | … | 0,12 | 1,2 | 12 | 120 | 1200 |

Logaritmering sänker räknesätten med ett "steg". Multiplikation blir addition, division blir subtraktion, potensupphöjning blir multiplikation, rotutdragning blir division.
Benämning och beteckning
Beteckningen logb aBeteckningen log aOm bx = a, kallas x logaritmen av a i basen b
(eller b-logaritmen för a) och man skriverx = logb a, (med äldre skrivsätt x = blog a eller x =
a)
T.ex.
log3 81 = 4, (logaritmen av åttioett i basen tre är fyra) eftersom 34 = 81,
log10 120 ≈ 2.07918.. (tiologaritmen för hundratjugio är …) eftersom 102.07918 ≈ 120
loga= -1, eftersom a-1 =
Produkter efter "log" beteckning behöver inte sättas inom parentes, då
logn ab = logn (ab) däremot a logn b = (logn b)·a = logn ba
Önskar man inte specificera basen, eller använder man bara ett bestämt logaritmsystem kan beteckningen log a används i stället för logn a.
Antilogaritmen för ett tal, det tal, vars logaritm (relativt någon bas) är det givna talet, dvs. det tal, som fås, om basen upphöjs till det givna talet.
t.ex. a är antilogaritmen för x om lg a = x, dvs. a = 10 x
1000 är antilogaritmen för 3 om basen är 10.
log ab = log a + log b Logaritmen av en produkt är summan av faktorernas logaritmer.
log= log b - log c Logaritmen av ett bråk är täljarens logaritm minus nämnarens logaritm.
log bn = n·log b Logaritmen av en potens är exponenten gånger basens logaritm.
Logaritmen av en rotstorhet är logaritmen av det tal man drar roten ur, dividerat med rotexponenten.
Logaritmering sänker räknesätten med ett "steg". Multiplikation blir addition, division blir subtraktion, potensupphöjning blir multiplikation, rotutdragning blir division.
Det finns ingen logaritmsats för en summa eller en skillnad (log (a+b) eller log (a-b) ).
Man kan inte ta logaritmen av ett negativt tal.
T.ex.:
log2![]() = log28 - log24 = 1,
= log28 - log24 = 1,
log (3x) = x·log 3
log pq²√r = log p + 2 log q + ½ log r
3x = 10 ![]()
![]()
Logaritmsystem
Med logaritmsystem förstås sammanfattningen av alla logaritmer, som hänföra sig till samma bas.
Man väljer för logaritmsystems bas enbart positivt tal skilt från 1, eftersom 1x = 1 oberoende av värdet på x och upphöjande från negativ bas resulterar komplext värde.
Logaritmerna är i allmänhet irrationella tal. Logaritmen för 1 är alltid 0. Om basen är större än 1, är logaritmerna för alla egentliga bråk negativa, men positiva för alla övriga tal.
T.ex. log2![]() = - 2
= - 2
Mellan två godtyckliga logaritmsystem med baserna a och c gäller sambandet:
![]()
Om man alltså har ett tals c-logaritm given och önskar erhålla samma tals a-logaritm, har man att antingen dividera med logca eller multiplicera med logac. Den storhet logac, som man har att multiplicera c-logaritmen för att få a-logaritmen, kallas för a-systemets modul (eller modyl) i förhållande till c-systemet.
Räkna ut exponenten
T.ex.
23x = 49 ![]() x = log23 49 =
x = log23 49 = ![]() =
=![]() ≈1,24121
≈1,24121
Bevisning:
23x = 49
(10k)x = 49 om 10k = 23
om 10k = 23 då k = lg 23
(10k)x = 10kx = 49
om 10kx = 49 då kx = lg 49
x = ![]() =
= ![]()
10-logaritm (lg)
Med 10-logaritmen (vanliga eller artificiella eller briggska logaritmen) för ett tal menas den exponent, man ska upphöja 10 till för att få talet. I stället för log10a skriver vi lg a
lg a = x är i ett annat skrivsätt: 10x = a
10-logaritmen av ett tal består av två delar:
1. Ett heltal, som kan vara positivt, negativt eller lika med noll (talet kallas karakteristikan) och
2. ett bråk i decimalform mellan 0 och 1 (bråket kallas mantissan).
T.ex. lg 120 ≈ 2.0791812460. Karakteristikan är 2, mantissan är 0.0791812460.
lg 0.12 ≈ -0.9208187539 Karakteristikan är -1, mantissan är 0.0791812460.
pH-värde
En lösnings surhetsgrad kan anges med ett pH-värde. Man har
pH = - lg [H+] där [H+] betyder vätejonkoncentrationen (i mol/dm³ eller M (molar)).
Vätejonernas koncentrationen är t. ex. 0,00001, dvs. 10-5. Då är pH = 5.
Naturlig logaritm (ln)
Naturlig logaritm (eller neppersk logaritm eller hyperbolisk logaritm) är logaritm med basen e ; företredsvis använd i teoretiska sammanhang.
Talet e (nepers tal) är ett gränsvärde.
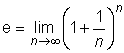 e:s närmevärde med tio decimaler är 2,7182818285
e:s närmevärde med tio decimaler är 2,7182818285
I stället för logea skriver vi ln a. (logarithmus naturalis)
ln a = x är i ett annat skrivsätt: ex = a
Logaritmiska storheter
Logaritmisk storhet är storhet uttryckt som logaritmen för kvoten av två storheter av samma slag, t ex två spänningar, två effekter, två frekvenser.decibel (dB)
är enhet för logaritmiska storheter; 1 decibel = 0,1 bel. För effektstorheter svarar 1 bel mot förhållandet 10 och 1 dB mot förhållandet 100,1≈1,259. För s.k. fältstorheter, t.ex. ljudtryck och elektrisk spänning, svarar 1 bel mot förhållandet 100,5≈3,162 och 1 dB mot 100,05≈1,122.
neper (Np)
är enhet storheter. 1 neper svarar mot kvoten e av två fältstorheter och kvoten e² av två effektstorheter.
1 neper = 2 lg e bel ≈ 8,686 db
1 bel = 0,5 ln 10 neper ≈ 1,151 neper
Fältstorhet är här en storhet vars kvadrat i linjära system är proportionell mot effekt eller energi, t ex spänning, ström, ljudtryck, elektrisk fältstyrka, partikelhastighet och laddningstäthet.
Effektstorhet är här effekt och storheter som är direkt proportionella mot effekt eller
energi, t ex energitäthet, ljudintensitet och ljusstyrka.
Fältstorheter och effekt storheter liksom deras kvoter kan vara komplexa (matematiskt sett)
och anges genom belopp och argument (vinkel).
Exemplar:
ljudintensitetsnivå: LI = 10 lg (I/Iref) dB, Iref ett valt referensvärde. Som referensvärde används 1 pW/m².
förstärkning (för fältstorhet): GF = 20 lg (F2/F1) dB = ln (F2/F1) Np
förstärkning (för effektstorhet): GP = 10 lg (P2/P1) dB = 0,5 ln (P2/P1) Np
Logaritmskala
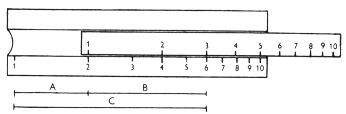
Räknestickan bygger på summering av logaritmer. Sliden och stickans fasta del är försedda med identiska logaritmiska skalor. Genom att sätta slidens etta över talet a på den fasta skalan, förflytta löparen till talet b på slidans skala läser man under löparstrecket resultatet av multiplikationen, talet c på den fasta skalan. |
 |
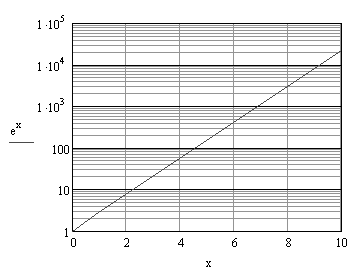 |
I en del tabeller förekommer ibland så stora variationer, att det blir svårt att återge dem grafiskt om likformig skala används. Det finns emellertid färdigtryckt rutat papper med logaritmisk skala antingen enbart i höjdled eller både på längden och också höjden. Grafen till en exponentialfunktion blir en rät linje om den ritas i ett koordinatsystem med logaritmisk skala på y-axeln. |
Logaritmekvationer
Ekvationer, som innehåller den obekanta under logaritmtecken, kallas logaritmekvationer. Dessa tillhör de transcendenta ekvationerna och kan grafiskt men ej algebraiskt lösas generellt.
Imaginära eller komplexa rötter måste alltid förkastas, då ju logaritmen för dylika tal ej definierats. Av de reella rötterna är ej heller med säkerhet alla användbara: Logaritmen existerar ju ej för negativa tal och om alltså en erhållen rot gör något av uttrycken under logaritmtecknet negativt, duger den ej som lösning till den givna ekvationen.
Ex 1. (med substitution)
![]()
![]() Sätt log x = y
Sätt log x = y
![]() (andragradsekvation)
(andragradsekvation)
varav y1 = 2 och y2 = ½
lg x1 = 2 och lg x2 = ½
x1 = 100 och x2 = ![]()
Ex 2.
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |