| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
|
Proportionslära Proportion (förhållande) - Analogi - Proportionalitet |
Proportionslära kallas läran om proportioners och proportionella storheters egenskaper. Denna lära behandlas av Euklides i femte boken av "Elementa", vilken till formen är geometrisk, men i sak tillhör både aritmetiken och geometrin.
Proportion
(ordet portion betyder andel)
1) I stället för benämning "förhållande" användes tidigare uttrycket "proportion" av det namnet proportionslära.
2) Med proportion menas man vanligen lika förhållande.
3) Likhet mellan två förhållanden kallas även analogi.
Förhållande (proportion)
Jämförelsen mellan två storheter (a, b) av samma slag, i anseende till deras storlek, kallas deras ration eller förhållande.
Förhållandet två storheter (a, b) emellan, utmärkes med kolonet (:), så a:b betyder det förhållande som a har till b.Exempel

a:b = 2:3 är samma som 3a = 2b
Med förhållandet mellan två tal menas talens kvot. (t.ex. 5 : 2 = 5/2)
Med förhållandet mellan två storheter menas kvoten mellan storheternas mätetal.
Förhållandet mellan två storheter är ett tal, en obenämnd storhet. Förhållandet mellan 7 kg och 5 kg t.ex. ![]()
Om storheterna är av samma slag, t. ex. två längder eller två volymer, måste de vara uttryckta i samma enhet.
Exempel
Förhållandet mellan 30 m och 2 m är 30:2=15.
Förhållandet mellan 30 m och 20 dm är 30:2=15.
Förhållandet mellan 30 m och 2 dm är 30:0,2=150.
Förhållandet mellan diagonalen och sidan i en kvadrat är √2:1 = √2
Lika (eller samma) förhållande
Proportion betyder även samma (eller lika) förhållande. De storheter, som är i samma förhållande, sägs vara proportionella.
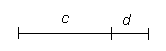
a : b = c : d (a förhåller sig till b som c till d)
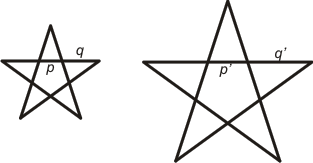 |
q:p=q':p' |
Om tre storheter (a, b, c) är proportionella, så
sägs den första (a) har den tredje (c) en duplicerad proportion av den, som hon har till den andra (b).
a:b=b:c
Om fyra storheter (a, b, c, d) är proportionella, så sägs den första (a) har till den fjärde (d) en triplicerad proportion av den, som hon har till den andra (b).
a:b=b:c=c:d
I två grupper av storheter y1, y2, y3 … yn och x1, x2, x3 … xn (n-tiplar) sägs y vara direkt proportionell med x, om varje lika indicerat par (yi och xi) gäller
yi : xi = en konstant = k
![]()
Om yi xi = k, sägs y vara omvänt proportionell mot x.
Analogi (The proportion)
Likhet mellan två förhållenden kallas även analogi. Således är a : b = c : d en analogi
Var och en av de fyra proportionella storheterna (a, b, c, d) kallas en proportional eller en term i analogien. MedelproportionalI analogien b2 = ac eller
Av tre på varandra följande tal (a1, a2, a3) i en geometrisk talföljd är den mittersta medelproportionalen till de två andra (geometriskt medelvärde). |
a : b = c : d eller
(a, b, c och d ≠ 0) (a förhåller sig till b som c till d) 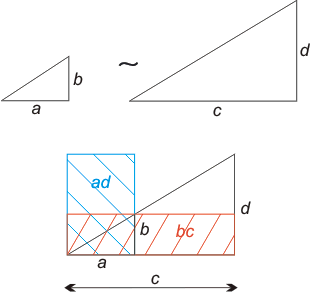 |
Satser om analogier |
Regula de tri, räknemetod som anger hur man från att känna tre av fyra tal a, b, c och d, som uppfyller a/b=c/d, bestämmer det fjärde. Metoden, som förr användes i matematikundervisningen, innebär att man stegvis resonerar sig fram till lösningen i stället för att ställa upp en ekvation.
Proportionalitet, samband mellan variabler
Direkt proportionalitet
Två storheter (variabler) sägs vara direkt proportionella om den ena storheten (beroende variabeln) blir N gånger större om den andra storheten (oberoende variabeln) blir N gånger större.
En direkt proportionalitet mellan x och y är ett samband av formen
k kallas för proportionalitetskonstant (eller proportionalitetsfaktor).
Proportionalitet betecknas med proportionalitetstecken: ~ eller
![]()
Som exempel på direkt proportionalitet kan nämnas:
väg och tid: s ![]() t (s = v·t)
t (s = v·t)
tyngd och massa: G ![]() m (G = g·m)
m (G = g·m)
pris och varumängd.
Omvänd (eller invers) proportionalitet
Två storheter sägs vara omvänt proportionella, om de beror så av varandra, att den ena blir N gånger mindre, när den andra blir N gånger större. Produkten av de två storheterna är konstant.
En omvänd proportionalitet mellan x och y är ett samband av formen
Som exempel på omvänt proportionella storheter kan nämnas:
arbetstid och antalet arbetare
rymd och tryck av en inspärrad gasmängd: ![]() (vid konstant temperatur, p·V = m·R·T).
(vid konstant temperatur, p·V = m·R·T).
Kvadratisk proportionalitet
Kvadratisk proportionalitet är ett samband av formen y = k·x2.Exempel: Rörelseenergin är proportionell mot kvadraten på hastigheten (Wk = ½·mv²)
Omvänd kvadratisk proportionalitet är ett samband av formen y = k/x²Exempel: Tyngden hos en kropp är omvänt proportionell mot kvadraten på avståndet till jordens medelpunkt. (![]() )
)
Skalanär (i samband med t ex kartor och ritningar) förhållandet mellan bildens och det avbildades dimensioner. |
 |
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |