| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
|
Kvadrat - Rektangel Romb - Romboid Parallellogram Deltoid - Trapets Omskriven fyrhörning |
Fyrhörning
(Tetragon)
|
Geometri - Grundbegrepp Polygon |
En fyrhörning eller fyrsiding eller tetragon (eng. Quadrilateral) är en polygon som begränsas av fyra sträckor, som kallas sidor, vilkas träffpunkter kallas hörn.
krosade fyrasidig som "Überschlagenes (överlappande) Trapez" och "Antiparallelogram" betracktas vanligen inte som fyrhörningar.
För fyrkant kallas i vardagsspråk de rättvinkliga fyrhörningar som rektangel och kvadrat.
Fyrhörningen benämns vanligen efter hörn t.ex. ABCD som vanligen betecknas motsols riktning.
konvex fyrhörning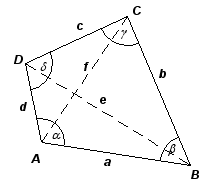
|
konkav fyrhörning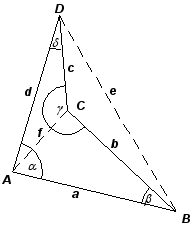
|
Motstående sidor i en fyrhörning är sidor som inte har gemensamma hörn.
Motstående vinklar i en fyrhörning är innervinklar som inte har gemensamma vinkelben. Vinkelsumman av innervinklarna i en fyrhörning är 360º.En diagonal i en fyrhörning är en rät linje, som förbinder två hörn utan att vara sida. Diagonalen delar fyrhörningen två trianglar. Summan (eller skillnaden) av trianglarnas area är fyrhörningens area. |
Kvadratsumman av sidorna
| där e och f är diagonaler m är avstånd mellan mittpunkter av diagonalerna. |
Arean av en konvex fyrhörning:
| där θ är vinkeln mellan diagonalerna (e och f) |
Brahmagupta formel:
![]()
där ![]() A och B är motstående vinklar.
A och B är motstående vinklar.
|
En parallellogram är en fyrhörning, där motstående sidor är parallella Varje kvadrat, rektangel, romb och romboid är parallellogram. Med en parallellograms bas(a, b) och höjd (ha, hb) förstår man en sida och dennas avstånd från den motstående sidan. |
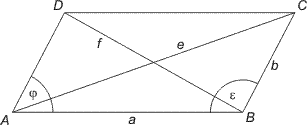 |
Samband mellan sidorna och diagonalerna (parallellogramlagen) är:
e2 + f2 = 2(a2 + b2)
Bevisning (tydliggörande):
e2 = a2 + b2 - 2ab·cos ε
(cosinussatsen i ABCΔ)
f2 = a2 + b2 - 2ab·cos φ
(cosinussatsen i ABDΔ)
cos ε + cos φ = 0
![]() ε = 180° - φ
ε = 180° - φ
I en parallellogram är motstående vinklar lika stora.
I en parallellogram är motstående sidor lika stora.
I en parallellogram halverar diagonalerna varandra.
Diagonalen delar en parallellogram i två kongruenta trianglar.
Om en vinkel i en parallellogram är rät, så är de övriga vinklarna också räta.
Om två närliggande sidor i en parallellogram är lika stora, så är parallellogrammen liksidig.
 |
Kvadrat
En kvadrat är en likvinklig och liksidig fyrhöring. Kvadraten är en regelbunden (reguljär) polygon. En kvadrat är en parallellogram i vilken närliggande sidor är vinkelräta och lika långa. |
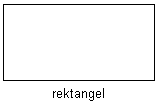 |
Rektangel
En rektangel är en likvinklig och oliksidig fyrhörning.En rektangel är en parallellogram i vilken närliggande sidor är vinkelräta men alla sidorna inte lika långa. Arean av en rektangel är de två närliggande sidornas produkt. Därför kallas även produkten av två längder för rektangeln. (se t.ex. i kordasats eller i Ptolemeiska sats) |
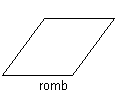 |
Romb
En romb är en liksidig och olikvinklig fyrhörning.En romb är en snedvinklig liksidig parallellogram. |
 |
Romboid
En romboid är en fyrhörning i vilken endast de sidorna och vinklarna, som stå mittemot varandra, är lika stora.En romboid är en snedvinklig oliksidig parallellogram. |
En fyrhörning utan parallella sidor kallas trapetsoid.
På amerikanska 'trapezoid' betyder (parallell)trapets och fyrhörningen utan parallella sidor kallas 'trapezium'.
I skolmatematiken betraktas en kvadrat som ett "specialfall" av en rektangel och en romb, motsatt till vanliga språkbruk och definitionerna i den Svenska Akademiska Ordbok, och definitionerna i Eukides' Elementa.
 |
"22 And of the quadrilateral figures: a square is that which is right-angled and equilateral, a
rectangle that which is right-angled but not equilateral, a rhombus that which is equilateral
but not right-angled, and a rhomboid that having opposite sides and angles equal to one
another which is neither right-angled nor equilateral. And let quadrilateral figures besides
these be called trapezia." (from Euclidis Elementa - with an accompanying English translation by Richard Fitzpatrick) |
Deltoid
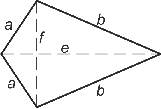 |
En deltoid är en fyrhörning i vilken endast en av de två diagonalerna är symmetriaxeln. I en deltoid är de motstående vinklarna och två-två av närliggande sidorna är lika stora. Den konvexa deltoiden kallas även drake. Diagonalerna av en deltoid är vinkelrätta. Arean av en deltoid är |
Parallelltrapets
| Ett trapets (parallelltrapets) är en fyrhörning, där ett par sidor är parallella. |
|
| Höjden (h) i ett trapets är avståndet mellan de parallella sidorna. | 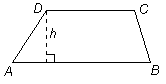 |
|
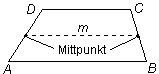
Medianen (m) i ett (parallell)trapets är den sträcka som förenar mittpunkterna på de båda icke-parallella sidorna, kallas även mittransversalen, halverar benet och diagonalerna och dess längd är hälften så stor som summan av längderna av de parallella sidorna, alltså m = Arean av ett trapets är halva summan av de parallella sidornas längder gånger höjden, alltså A = |
 |
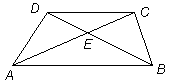
| Diagonalerna i ett trapets delar varandra i delar, som hörhåller sig som de parallella sidorna: |
 |
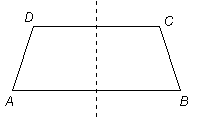
| Likbent trapets Om de icke parallella sidorna är lika stora, kallas trapetsen likbent. Ett likbent trapets har en symmetriaxel. I ett likbent trapets är diagonalerna lika långa. I ett likbent trapets är vinklarna vid basen lika stora. I ett likbent trapets är motstående vinklar supplementvinklar - trapetset går alltså att inskriva i en cirkel. |
 |
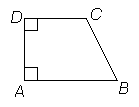
| Rätvinkligt trapets har två rätvinkliga vinklar. |
|
Omskriven fyrhörning är en fyrsidig omskriven polygon, den kallas även för tangentfyrhörning.I en omskriven fyrhörning är summorna av motsatta sidor lika stora. a + c = b + d |
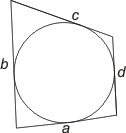 |
Kvadrat, romb, och drake (konvex deltoid) är tangentfyrhörningar.
Cirkelfyrhörning eller inskriven fyrhörning En fyrhörning kallas inskriven (eller cyklisk) om dess hörn ligger på en cirkel.
|
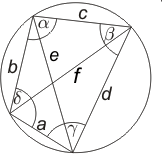 |
Kvadrat, rektangel och likbent trapes är cirkelfyrhörning.
Symmetriska fyrhörningar
Symmetriska fyrhörningar har symmetriaxel (symmetriaxlar):
| Kvadrat | har fyra symmetriaxlar |
| Rektangel och romb | har två symmetriaxlar |
| Deltoid och likbent trapets | har en symmetriaxel |
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |