WolframAlpha| WolframAlpha |
Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
 Gästbok |
Nedladdning
|
|
|
Korda, sekant Medelpunktsvinkel, bågvinkel Kordasats |
Cirkel | Cirkelns ekvation Kägelsnitt - andragradskurvor Geometri - Grundbegrepp |
Cirkellinje
Cirkeln är en plan sluten kurva, en kroklinje vars alla punkter har samma avstånd till en given punkt, cirkelns centrum eller medelpunkt. En rät linje, dragen från medelpunkten till en punkt på cirkeln, kallas radie. Även längden av en sådan sträcka kallas radie.
  |
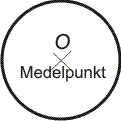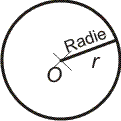Cirkeln är den geometriska orten för alla punkter som har samma avstånd till en given punkt. Medelpunkten vanligen betecknas med O (origo = ursprung), det är en utgångspunkt för alla radier (radius = stråle). |
Cirkeln är en s.k. andragradskurva, som i kartesiska koordinater har ekvationen
(x - x0)² + (y - y0)² = r²,
där (x0, y0) är cirkelns centrum och r dess radie.
Ekvationen x² + y² + px + qy + s = 0 betyder en cirkel. (p, q, s är konstanter)
Cirkelområde
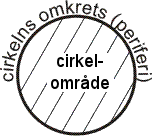
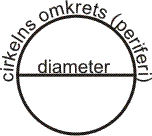
Med cirkel avses ibland som plan figur, den av kurvan inneslutna ytan (cirkelområde). Kurvan själv kallas då cirkelns periferi och dess längd cirkelns omkrets. En rät linje, dragen mellan två punkter på periferin genom cirkelns centrum, kallas diameter. Även diameterns längd kallas diameter.
Talet π (pi)
Förhållandet mellan en cirkels omkrets och dess diameter är talet π (pi).
Talet kallas även Arkimedes konstant eller Ludolphs tal.
Detta tal kan inte uttryckas med ett ändligt antal decimaler; ett approximativt värde är 3,14159265…
π är en grekisk bokstav (läses pi) och den används i stället för 3,14159265…. I vanliga fall tar man med endast två decimaler, alltså 3,14, eller också räknar man med bråket 22/7, som är mer exakt än 3,14.
En cirkel med radien r har omkretsen 2π r och arean π r 2.
 |
 |
Exemplar för numerisk beräkning av π:
Leibinz serie:
Wallins produkt:
Cirkelbåge
 |
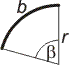En cirkelbåge är en sammanhängande del av cirkeln. Båglängden, som svarar mot en vinkel (medelpunktsvinkeln) på β , är b = r·β, där r är radie och β är vinkeln i bågmått; eller om vinkeln i gradmått.
|
Korda, sekant
 |
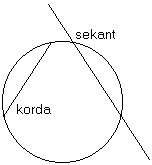Korda är en sträcka mellan två punkter på cirkelns periferi. En sekant är en rät linje som skär cirkeln i två punkter. En korda delar cirkelområdet (cirkelskivan) i två områden, som kallas segment. |
 |
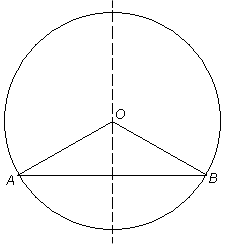Om en diameter är vinkelrätt mot en korda, så är den kordans mittnormal och bisektris till den mot kordan svarande medelpunktsvinkeln. En kordas mittnormal är alltid en diameter i cirkeln. Denna egenskap innebär även, att cirkelns medelpunkt ligger på kordans mittnormal. Den räta linje, som förbinder medelpunkten med en kordas mittpunkt, är tillika vinkelrätt mot kordan, d.v.s. dennas mittnormal. |
Cirkelsegment
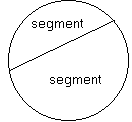
Ett segment är ett område som begränsas av en cirkelbåge och en korda mellan bågens ändpunkter.
 |
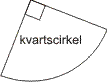
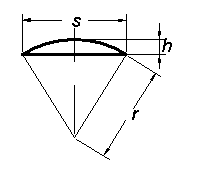Radie: |  |
Arean: |
  där b är båglängd |
| Bågens höjd: |  |
|||
| Kordans längd: | 
|
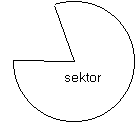
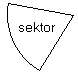
Cirkelsektor
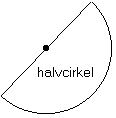
En cirkelsektor (sektor) är ett område som begränsas av en cirkelbåge och radierna till bågens ändpunkter. Om radierna tillsammans utgör en diameter är sektorn en halvcirkel. Halvcirkeln kan också uppfattas som ett segment. En fjärdedels cirkel kallas kvartscirkel.
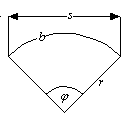Arean av en cirkelsektor är 
Tangent till en cirkel
En tangent till en cirkel är en rät linje, som går genom en punkt på cirkeln (tangeringspunkten). Tangenten är vinkelrätt mot radianen i tangeringspunkten.
 |
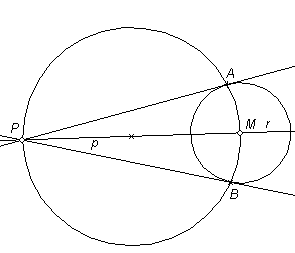Att genom en given punkt utom en given cirkel dragna tangenter till cirkeln Sammanbind den givna punkten P med den givna cirkelns medelpunkt M. Uppslå på PM såsom diameter en cirkel p. Om denna cirkels skärningspunkter A och B sammanbindas med P, så är PA och PB de sökta tangenterna, då vinklarna PAM och PBM, som står i halvcirklar är räta. |
Medelpunktsvinkel, bågvinkel
 |
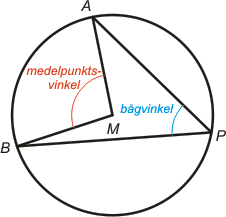Vinkeln mellan radierna genom en båges ändpunkter kallas medelpunktsvinkel till bågen. Vinkeln mellan två kordor, vars spets ligger på cirkelns periferi kallas bågvinkel (periferivinkel eller randvinkel eller omkretsvinkel). Om bågen AB ligger inom vinkeln APB och P är en punkt på cirkelns periferi, som inte tillhör bågen AB, sägs bågvinkeln (periferivinkeln) APB stå på bågen AB. Bågvinkelsatsen (periferivinkelsatsen) I en cirkeln är bågvinkel hälften så stor som medelpunktsvinkeln till samma båge. Följdsatser: (av bågvinkelsatsen)
|
|
Kordavinkel Spetsen innanför cirkelperiferin, benen är kordor |
 |
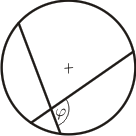Kordasatsen
|
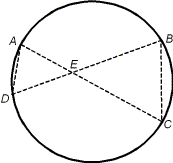
Om två kordor i en cirkel skära varandra (inuti eller utanför cirkeln), så är rektangeln (eller produkten) av den ena kordans segment är lika med rektangeln av den andra kordans segment.
EA·EC = EB·ED Bevisning: Eftersom vinklarna DAC och CBD är randvinklar på samma båge, är de lika. Analogt är vinklarna ADB och BCA lika. Därmed är trianglarna ADE och BCE likvinkliga och, enligt tredje likformighetsfalet, likformiga. Följdsats. (Tangent-sekant sats) Om från en punkt utanför en cirkel en tangent och en sekant till cirkeln är dragna, så är kvadraten på tangenten är lika med rektangeln (eller produkten) av hela sekanten och dess utanför cirkeln liggande del. EA² = EB·ED En korda t ex EAC utgör en tangent till cirkeln, varvid punkterna A och C sammanfaller. |
 |
|
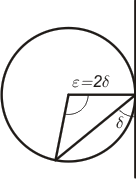
Kordatangentvinkel Spetsen på cirkelperiferin, det ena benet är en korda, det andra en tangent. En kordatangentvinkel är hälften så stor som medelpunktsvinkeln till kordans ändpunkter. |
 |
|
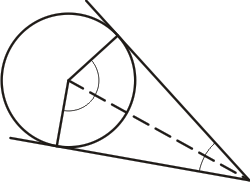
Tangentvinkel Spetsen utanför cirkelperiferin, benen är tangenter. En tangentvinkel är 180º minus medelpunktsvinkeln till tangeringspunkterna. |
 |
|
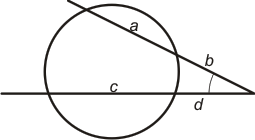
Sekantvinkel Spetsen utanför cirkelperiferin, benen är sekanter.Sekantsatsen: (a + b)·b = (c + d)·d |
 |
 |
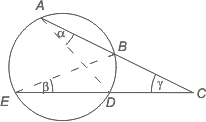Dra linje mellan A och D, och mellan B och E, då CADΔ ~ CBEΔ eftersom α=β (bågvinklar) och γ=γ (gemensam vinkel), då AC : DC = EC : BC varifrån AC · BC = EC · DC |
|
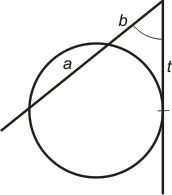
Sekanttangentvinkel Spetsen utanför cirkelperiferin, det ena benet är en sekant, det andra en tangent.Tangent-sekant-satsen: t² = (a + b)·b |
 |
|
Koncentriska, excentriska cirklar Två cirklar med samma medelpunkt kallas koncentriska, (två sådana med olika medelpunkter excentriska). Det plana område som begränsas av två koncentriska cirklar kallas cirkelring. |
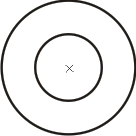 koncentriska cirklar |
 excentriska cirklar |
|
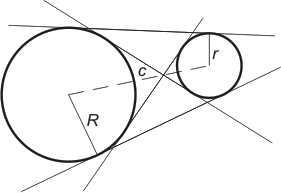
Centrallinje Den linje, som förbinder de två cirklarnas centra, kallas centrallinjen (c), och cirklarnas radier betecknas vanligen med R och r.Om c > R + r |
 |
|
Tangerande cirklar Två cirklar som har en punkt gemensam och där har samma tangent sägs tangera varandra. |
 |
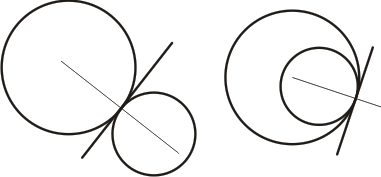| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |
