WolframAlpha Lexikon Formler Terminologi länkar Svenska matematiklänkar Math. Resources on the Internet Böcker

Gästbok
Matematik minimum - Terminologi
En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik
A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö     
Klicka på någon av bokstäverna
 Nedladdning

Koordinatsystem i planet

Analytisk geometri

Analytisk geometri, den gren av geometrin i vilken man studerar räta linjer, kurvor, plan och ytor med hjälp av koordinatsystem och elementär algebra.

Genom ett koordinatsystem införs ett samband mellan geometrins grundläggande element, punkter, och algebrans fundamentala begrepp, tal, varigenom man kan använda algebrans metoder på geometrins problem.

Rätvinkliga (kartesiska) koordinater

Koordinataxlar
Två linjer (koordinataxlar), som inte är parallella och nollpunkter i skärningspunkten, bildar ett koordinatsystem.
Linjernas positiva riktningar utmärks med pilar. Den vågräta axeln kallas x-axeln, abskissan eller första axeln, den lodräta y-axeln, ordinatan eller andra axeln. Första axeln ritas vanligen riktad åt höger och andra axeln riktad uppåt. Ett sådant koordinatsystem sägs vara positivt (motsols, moturs eller vänstervarv) orienterat.

Ortonormerat
Om tallinjerna (talaxlarna) är vinkelräta mot varandra och längdenheterna är lika kallas koordinatsystemet ortonormerat.

Origo - kvadranter
Koordinataxlarnas skärningspunkt kallas origo och betecknas med stort O. De fyra delarna som begränsas av axlarna kallas 1:a, 2:a, 3:e och 4:e kvadranterna.

Koordinat

I ett koordinatsystem, vart och ett av de tal som används fär att ange en punkts läge.
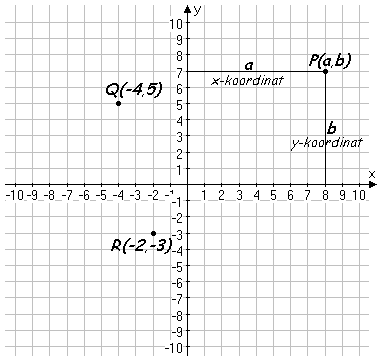
Man kan ange en punkts läge i planet genom att tala om,
  • hur långt den ligger från y-axeln (punktens x-koordinat, abskissan för punkten)
  • och hur långt den ligger från x-axeln (punktens y-koordinat, ordinatan för punkten).
Den punkt vars koordinater är a och b kallas ofta punkten (a, b) vilket utläses "punkten a b".

Vill man ange P:s läge, skriver man: P(a, b).
De två talen (bokstäverna) i parentesen kallas punkten P:s koordinater.

Koordinaterna åtskils vanligen med kommatecken.
För att undvika förväxling med decimalkomma kan man i stället använda semikolon.
T.ex.: P(1.5; -2.3)

Koordinattransformation

Parallellförskjutning av koordinatasystemet

Om (x0, y0) är koordinaterna för origo i det nya systemet, så gäller:

x' = x - x0;       y' = y - y0

Vridning av koordinatsystemet

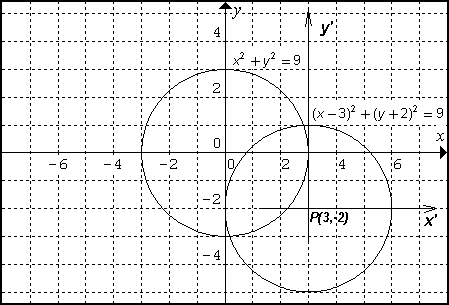
Räknas vridningsvinkeln α positiv i positiv led (dvs. den riktning, positiva x-axeln behöver vridas 90° för att övergå i positiva y-axeln), så bli transformationsformlerna:

 

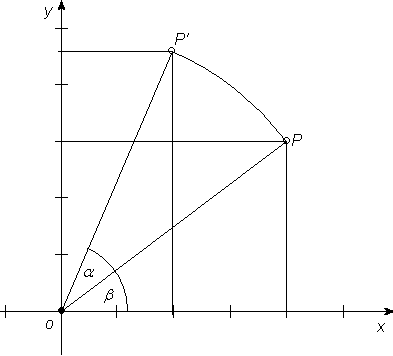OP' = OP
x = OP cos β
x' = OP' cos (α + β)
 y = OP sin β
y' = OP' sin (α + β)
x' = OP cos α cos β - OP sin α sin β
y' = OP sin α cos β + OP cos α sin β

Polära koordinater

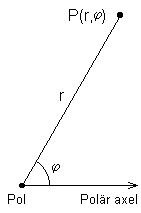Plana polarkoordinater: en punkts läge bestämmes i ett plan dels genom avståndet från punkten till en fix punkt i planet (polen), dels genom den vinkel mellan linjen genom punkten och polen samt en fix stråle med polen som begynnelsepunkt (polära axeln).

Låt P vara en given punkt i planet. Sträckan från polen till P kallas radius vektor för P. Punkten P:s läge ges av längden r av radius vektor och vinkeln φ mellan polära axeln och radius vektor.
Paret (r, φ) kallas de polära koordinaterna för P.

För att skilja från de rätvinkliga koordinaterna
betecknas de polära koordinaterna ibland med (r  φ)

Om ett ortonormerat koordinatsystem införs i det polära koordinatsystemet så att origo och pol sammanfaller och så att den polära axeln sammanfaller med positiva x-axeln, fås koordinattransformationen mellan de båda systemen av ekvationerna:

x = r · cos φ y = r · sin φ
T.ex.: P(3, 5) P(5,830952 59,036243º)
Q(6 60º) Q(3; 5.196152)
av Bruno Kevius
All kopiering tillåten!   
 Matematiklexikon:
A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö
Klicka på någon av bokstäverna		    Svenska Matematiklänkar