| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
Vektor, vektorstorheter
|
Tredimensionella koordinatsystem Rymdgeometri |
Skalärer
Storheter som kan uttryckas med ett enda talvärde. t. ex. längd, värmemängd, volym kallas skalärer.
Storheter som uttryckas med komplexa tal är skalära. T.ex. Impedans (Z = R + jX).
Vektorer
Storheter som inte kan uttryckas med ett enda talvärde, kallas vektorer. Sådana är kraft, hastighet, acceleration, moment, fältstyrka etc. En vektor representeras av en sträcka till vilken man ordnat en viss riktning. Två vektorer är alltså lika om och endast om de har samma längd (storlek) och samma riktning.
Formellt kan vi definiera en vektor som en ordnad talmängd. Det betyder att två vektorer är identiska då (och endast då) de innehåller samma tal tagna i samma ordning. (2,4) är alltså inte samma vektor som (4,2).
En vektor kan betecknas med en bokstav med pil över (![]() ). Ett vanligt sätt att skriva vektorer i en text är a (fetstil).
). Ett vanligt sätt att skriva vektorer i en text är a (fetstil).
En vektor i planet och i rymden skrivs ofta v för att skilja den från skalärer, som är (reella) tal, ofta skrivna med grekiska bokstäver.
Vektorns riktning och längd En vektor 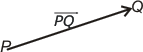 Om O är en fix punkt i planet eller rummet svarar till varje punkt P i planet resp. rummet en vektor
|
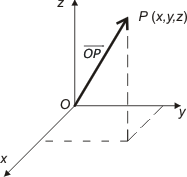 |
En s. k. fri vektor kan tänkas placerad i vilken punkt som helst i rummet.
De i fysiken förekommande vektorerna är dock i allmänhet ej fria
utan tänkas placerade i en viss punkt.
En vektor av längden 1 kallas enhetsvektor och betecknas
![]() (e). En godtycklig vektor
(e). En godtycklig vektor
![]() med riktningen
med riktningen
![]() och absoluta beloppet |
och absoluta beloppet |![]() | kan också skrivas:
| kan också skrivas:
![]() Således
Således 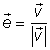
Två vektorer sägs vara lika, om de har samma längd och samma riktning. En vektor av längden 0, för vilken alltså begynnelsepunkt och ändpunkt sammanfaller, kallas nollvektor.
Nollvektorn är definierad enbart för räkningens skull, saknar både längd och riktning.
|
Komponent Om
Vektorerna x Då basvektorerna är fastslagna kan beteckningen
De tal som ingår i vektor kallas komponenter. |
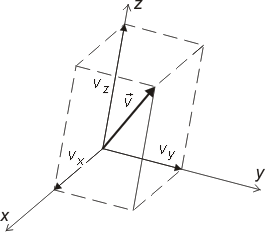 |
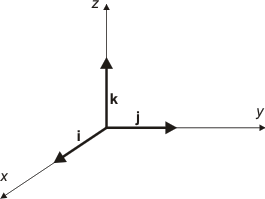
Basvektorer i tredimensionella orthonormerad koordinatsystem betecknas ofta med: i, j, k och komponenter skrivs med index. u = u1i + u2j + u3k = (u1, u2, u3) och längden för vektorn beräknas enligt |
 |
Operationer med vektorer
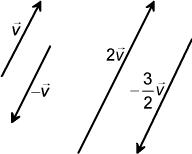
Multiplikation med skalär| Om
Parallella vektorer Två vektorer
|
 |
Addition av vektorer
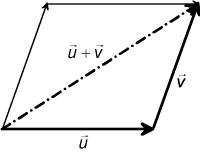
Termerna i vektoraddition kallas komposanter, och summan kallas resultant.Parallellogrammetoden:
Med ![]() +
+![]() menas den vektor, som är diagonal i den parallellogram, vars sidor är vektorerna
menas den vektor, som är diagonal i den parallellogram, vars sidor är vektorerna
![]() och
och
![]() .
.
Polygonmetoden:
Vektorerna ritas efter varandra i godtycklig ordning. Resultantens vektor går från utgångspunkten till den sist ritade vektorn. Om denna spets sammanfaller med utgångspunkten, dvs om vektorpolygonen sluter sig, är resultanten noll.
| Parallellogrammetod | Polygonmetod | |
 |
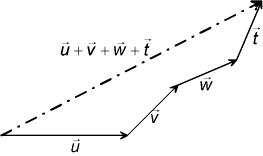 |
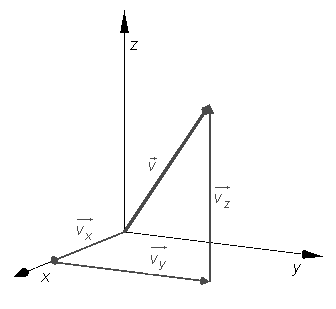 |
Man har: ![]() +
+ ![]() = (ux, uy, uz) + (vx, vy, vz) = (ux + vx, uy + vy, uz + vz)
= (ux, uy, uz) + (vx, vy, vz) = (ux + vx, uy + vy, uz + vz)
Subtraktion av vektorer
Vektorn ![]() -
-![]() =
=![]() + (-
+ (-![]() ) betraktas som summan av vektorn
) betraktas som summan av vektorn
![]() och (-
och (-![]() )
)
Räkneregler
|
|
= | |
| = | ( |
|
| λ( |
= | λ |
| = | 0 |
Triangelolikheterna:
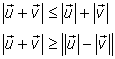
Lineära samband:
Om för två vektorer
![]() och
och
![]() gäller: λ
gäller: λ![]() + μ
+ μ![]() =0, där λ och μ är skalärer, är vektorerna parallella.
=0, där λ och μ är skalärer, är vektorerna parallella.
Om tre vektorer
![]() ,
,
![]() och
och
![]() gäller:
λ
gäller:
λ![]() + μ
+ μ![]() + ν
+ ν![]() = 0, där λ, μ och ν är skalärer, så ligger vektorerna i ett plan.
= 0, där λ, μ och ν är skalärer, så ligger vektorerna i ett plan.
Om ![]() ,
,
![]() ,
,
![]() och
och
![]() är 4 godtyckliga vektorer, kan man finna 4 skalärer α, β, γ, och δ, så att
är 4 godtyckliga vektorer, kan man finna 4 skalärer α, β, γ, och δ, så att
α![]() + β
+ β![]() + γ
+ γ![]() + δ
+ δ![]() = 0.
= 0.
Härav följer att en godtycklig vektor
![]() kan framställas med hjälp av 3 enhetsvektorer.
kan framställas med hjälp av 3 enhetsvektorer.
Linjärt beroende och linjärt oberoende
Om tre 3-dimensionela vektorer ligger i samma plan kan alltid en av vektorerna skrivas som linjär kombination av de två andra:
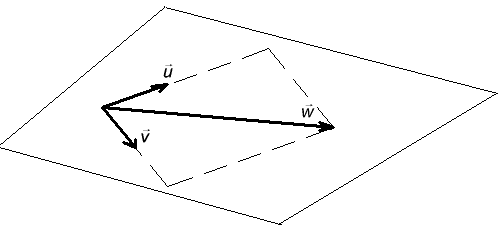
Man säger att
![]() ,
,
![]() och
och
![]() är linjärt beroende.
är linjärt beroende.
För godtyckligt antal dimensioner säger man att vektorerna v1, v2 … vn är
linjärt beroende om λ1v1 + λ2v2 + … + λnvn = 0 för en svit skalärer λ1, λ2 … λn där inte alla är = 0.
I annat fall är vektorerna linjärt oberoende.
En vektor är alltid linjärt oberoende om den inte är
nollvektorn.
Två vektorer är linjärt oberoende om och endast om de inte är parallella.
Tre vektorer är linjärt oberoende om och endast om de inte ligger i plan.
Skalärprodukt (Inre produkt eller punktprodukt)
Beteckna med φ vinkeln mellan
Skalärprodukten
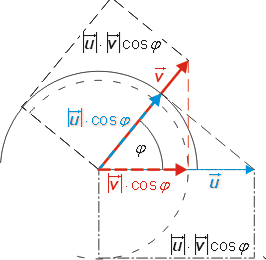
Geometriskt kan punktprodukten tolkas som projektionen av den ena vektorn på den andra. Om vektorerna definieras med koordinaterna (xu, yu, zu), (xv, yv, zv) för sina ändpunkter (vektorerna placerade i origo) blir skalärprodukten:
u·v = (u1i + u2j + u3k)·(v1i + v2j + v3k) = u1v1 + u2v2 + u3v3 eftersom |
 |
Räkneregler
|
|
= | |
| = | ||
| λ |
= | λ( |
|
|
= | 0, om |
Ex.: Mekaniskt arbete vid s förflyttningen av en kropp mot F kraft: W = F·s
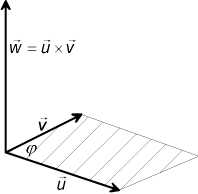
Vektorprodukt (Yttre produkt eller kryssproduk)
Med vektorprodukten
| u×v = (u1i + u2j + u3k)×(v1i + v2j + v3k) = (u2v3 - u3v2)i + (u3v1 - u1v3)j + (u1v2 - u2v1)k Eftersom Ofta skrivs vektorprodukten i komponent form med hjälp av en determinant:
Räkneregler
|
 |
Ex.: Vridmomentet för kraften
![]() med hävstångsarmen
med hävstångsarmen
![]() omkring vridningspunkten är
omkring vridningspunkten är
![]() .
.
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |