WolframAlpha Lexikon Formler Terminologi länkar Svenska matematiklänkar Math. Resources on the Internet Böcker

Gästbok
Matematik minimum - Terminologi
En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik
A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö     
Klicka på någon av bokstäverna
 Nedladdning

riktningscosiner
Tredimensionella koordinatsystem
 Analytisk geometri

Parallellkoordinater i rymden

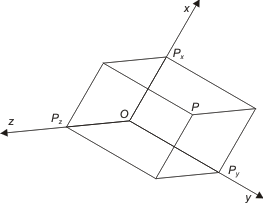
Vi betraktar tre plan, som råkas i en punkt O och som skär varandra två och två längs räta linjer, som vi betecknar som x-, y- och z-axlarna. På var och en inför vi en positiv riktning och en enhetssträcka. Vi har då i vart och ett av de tre planen ett koordinatsystem; i planet genom x- och y-axlarna (kortare: xy-planet) det koordinatsystem, som är bestämt av dessa båda axlar, o. s. v. Tillsammans utgör de tre axlarna ett koordinatsystem i rymden: O är origo (nollpunkten), axlarna koordinataxlar, planen koordinatplan.
Är P en godtycklig punkt i rymden, så lägger vi genom P planet || yz-planet; det skär x-axeln i Px. Vidare genom P planet || zx-planet, som skär y-axeln i Py, och planet || xy-planet, som skär z-axeln i Pz. Vi sätta
x = OPx ,  y = OPy ,  z = OPz ,
varvid OPx har det tecken, som svarar till den antagna positiv riktningen på x-axeln, och mätes med enhetssträckan på denna axel; analogt för OPy och OPz. Vi får då tre tal x, y, z, punkten P:s koordinater i det använda koordinatsystemet Oxyz. Mot varje punkt svarar på detta sätt ett tripel av tal (x, y, z).

Kartesiska (rätvinkliga) koordinater

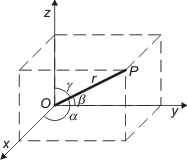
Som koordinatsystem i rymden används tre plan, parvis vinkelräta mot varandra. Planens skärningslinjer kallas x-, y- och z-axlarna. De tre planen benämns efter ingående axlar xy-planet, yz-planet och xz-planet. Systemet sägs vara ett högersystem, om en positiv rotation av 90º omkring x-axeln överför positiva y-axeln i positiva z-axeln.

I ett högersystem motsvaras x-, y-, och z-axlarna av högra handens tumme, utsträckta pekfinger och långfinger och på motsvarande sätt används vänsterhanden i ett vänstersystem.

Riktningscosiner

En punkt P:s koordinater (x, y, z) är vinkelrätta avstånden från P till yz-, xz-, och xy-planen. Med α, β, och γ betecknas vinkel mellan riktningen OP och axlarna.
Om OP = r, har man x = r cos α, y = r cos β och z = r cos γ.
cos α, cos β och cos γ kallas för riktningscosiner och betecknas a, b och c.
Man har: a² + b² + c² = 1       (cos² α + cos² β + cos² γ = 1)

Om två riktningar är givna: OA med riktingscosinerna a, b, c och OA1 med riktningscosinerna a1, b1, c1 gäller för vinkeln φ mellan OA och OA1:
cos φ = aa1 + bb1 + cc1

Komponenterna av en enhetsvektor e = (ex, ey, ez) med samma riktning är ekvivalenta de relevanta riktningscosinerna.
Även med vektor P = (Px,Py,Pz) kan man definiera riktningscosinerna som:

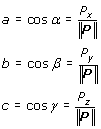
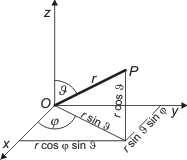
Sfäriska (polära) koordinater

P:s läge anges med
  1. längden av radius vektor OP = r
  2. vinkeln φ mellan x-axeln och projektionen av radius vektor på xy-planet
  3. vinkeln mellan radius vektor och z-axeln
Sambandet med rätvinkliga koordinater är:
x = r cos φ sin
y = r sin φ sin
z = r cos

Cylindriska koordinater

Läget av en punkt P i rummet bestäms

av dess avstånd z (med tecken) från xy-planet och
de polära koordinaterna (, φ) för dess projektion i xy-planet.

Sambandet med rätvinkliga koordinater är:
x = cos φ
y = sin φ
z = z

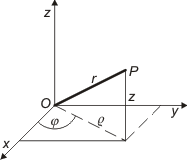Bokstavsbeteckningar för koordinater (x, y, z; r, φ, och , φ, z) är enligt svenska standarden SIS 01 41 11

 

av Bruno Kevius
All kopiering tillåten!   
 Matematiklexikon:
A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö
Klicka på någon av bokstäverna		    Svenska Matematiklänkar