| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
|
konstant variabel parameter storhetsvärde enhet |
Storhet (Kvantitet) Vetenskapen om storheter benämnes matematik |
Geometriska storheter SI enheter |
Storhet
(eng: quantity, fr: grandeur, ty: Größe, norsk: størrelse)
Kvantitet [av latin quantitas] är storhet, storlek, myckenhet, mängd.
Kvalitet [av latin qualitas] är beskaffenhet, egenskap (ofta motsats till kvantitet).
Länkar: Den matematiska storheten och erfarenheten (av Henri Poincaré).
Magnitude (Quantity) (från Book I of Hegel's Science of Logic - Being)
En storhet (eller kvantitet) är en egenskap hos ett föremål eller en företeelse som kan mätas eller beräknas.
Storhet är allt det som, genom likartade delars tilläggande eller borttagande, kan ökas eller minskas.
De storheter, om vilka man kan begripa, att den mindre kan tas så många gånger, att den blir större än den större, sägs vara av samma slag.
Storhetsslag
Storheter som kan jämföras med varandra tillhör samma storhetsslag.
Ett storhetsslag är en sammanfattning av storheter som på ett meningsfullt sätt kan kvantitativt jämföras med varandra.
(Sort är äldre ord för storhetsslag.)
Exempel: Längd, volym, hastighet och kraft utgör skilda storhetsslag, eftersom man ej kan jämföra t ex en längd med en kraft. En bredd b, höjd h, tjocklek d, radie r och en punkts tre kartesiska rumskoordinater x, y och z är skilda storheter av samma storhetsslag, nämligen längd.
En mindre storhet, som mäter det är jämnt innehålls i en större, kallas part (del) av den större; och den större åter, som mäts av den mindre, kallas då mångfaldig (multipel) av den mindre.
Om den mindre storhet innehålls tre gånger i en större, så kallas den mindre en tredjedel (tredjepart) av den större, och den större åter trefaldig (tredubbel) av den mindre, o. s. v. Eller i allmänhet: om b innehålls n gånger i a, så är b en n:te del (1/n) av a, och a åter n-faldig av b; varifrån n-faldig storhet av b betyder detsamma som b multiplicerad med n.
De storheter mellan vilka förhållandet med fullkomlig noggrannhet kan förekomma, eller som har ett gemensamt mått, kallas kommensurabla (mätbara). Men det ges storheter av samma slag, mellan vilka förhållandet icke kan exakt förekomma, fastän man dock kan komma detta förhållande så nära man behagar, och eftersom dessa storheter alltså icke har något gemensamt mått, så sägs de vara sinsemellan inkommensurabla (omätbara). T.ex. om förhållandet mellan sidan och diagonalen i en kvadrat skulle sökas, så finner man, att sidan : diagonalen = 1 : √2; men nu kan icke √2 exakt uttryckas, utgör sidan och diagonalen i en kvadrat inkommensurabla storheter.
En storhet kan vara konstant eller variabel.
En storhet kan vara skalär eller vektor.
En storhetsvärde kan vara bekant eller obekant.
Ett tal är en obenämnd storhet.
Kvantor
eller kvantifikator i logiken (och vanligen används ordet i modern matematik) en operator som binder en storhet och därvid bildar ett uttryck vars giltighet beror på antalet objekt som satisfierar det okvantifierade uttrycket.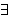 ! eller
! eller Konstant
Konstant är en matematisk storhet, (ett tal) med ett bestämt (konstant) värde.
Motsats är variabel, en storhet som förändras.
Konstanter betecknas ofta med alfabetets första bokstäver, a, b, c, d (även k, l, m, n).
Variabel
Variabel (föränderlig storhet) är en storhet (ett tal) som kan anta olika värden. Den har intet bestämt värde.
En variabel betecknas ofta med bokstäverna x, y eller z.
Oftast variera variablerna på sådant sätt, att de kunna anta alla värden mellan två gränser (i ett intervall). Man säger då, att variabeln förändras kontinuerligt, dvs. variabeln kan anta alla såväl rationella som irrationella värden, som finnas mellan de två gränserna.
Om vi tänker oss, att vi har alla tal ordnade på en linje (en s.k. tallinje), så motsvarar varje punkt på linjen av ett tal. Om nu x varierar kontinuerligt, t.ex. från 1 till 3, betyder det, att x genomlöper alla punkter mellan 1 och 3 på tallinjen.
En variabel, som ej genomlöper alla punkter utan hoppar över en del, kallas diskontinuerlig.
Parameter
Parameter är en matematisk storhet som betraktas som en konstant men som kan anta olika värden t.ex. i en ekvation eller en funktion.
I ekvationen för en rät linje, y = ax + b, är a och b parametrar. Även väntevärde och varians i en statistisk fördelning kallas parametrar. Inom fysiken talar man om fysikaliska parametrar, t.ex. temperatur, tryck och fuktighet, som bestämmer egenskaperna hos ett fysikaliskt system.
I den analytiska geometrin är parameterekvationerna för en plan kurva två ekvationer som uttrycker koordinaterna x och y för en punkt på kurvan i beroende funktioner av en gemensam variabel, kallad parameter. (t. ex. x = r · cos t, y = r · sin t)
För parameter kallas även en korda genom brännpunkten hos andragradskurvor.
Skalär, vektor, tensor
Skalära storheters värde anges med ett enda (reellt eller komplext) tal.
Storheter som inte kan uttryckas med ett enda talvärde, kallas vektorer.
Tensor i matematiken en uppsättning tal som transformeras enligt bestämda regler vid byte av koordinater. Det antal index som krävs för att ange dessa tal kallas tensorns ordning. En vektor v med koordinaterna vi är en tensor av ordning ett. En matris A med elementen aij är en tensor av ordning två. En tensor av ordning noll är detsamma som en skalär.
Storhetsvärde
Storhetsvärde (eller storlek) är ett visst kvantitativt fall av en storhet.
Bredden av ett visst bord, utbredningshastigheten hos elektromagnetiska vågor i fria rymden.
En storhetsvärde kan uttryckas som produkten av ett tal (mätetal) och en (mått)enhet.
Ett storhetsvärde kan vara bekant och obekant.
Exempel
| för en bekant storhet: | 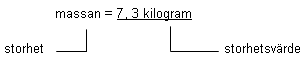 |
| för en obekant eller en given storhet: |
Ett visst storhetsvärde är helt oberoende av hur det uttrycks, eller om det över huvud taget uttrycks kvantitativt; ett bord är lika högt vare sig höjden eller anges som 0,914 4 m, 914,4 mm, 3 ft (engelska fot) eller 36 in (engelska tum).
Mått eller mätvärde är ett storhetsvärde uttryckt i mätetal och enhet.
Ett mätvärde är produkten av ett mätetal och en enhet.
| Mätvärde | mätetal | enhet | |||
| Konkreta storheter |
25 cm | = | 25 | · | 1 cm |
| 13 kg | = | 13 | · | 1 kg | |
| 60 s | = | 60 | · | 1 s | |
| Abstrakta storheter |
16 | = | 16 | · | 1 |
| 3/4 | = | 3 | · | 1/4 | |
| 16 a.e. | = | 16 | · | 1 a.e. (areaenhet) |
Enhet, måttenhet
En enhet är ett fixerat storhetsvärde (jämförelsevärde), som används för att numeriskt uttrycka andra storhetsvärden av samma slag, och har ofta standardiserad beteckning.
Enhet kan kännetecknas av benämning eller beteckning.
Exempel: För massa, massan av den internationella kilogramprototypen (kilogram, kg),
för kraft, den kraft som ger en kropp med massan 1 kilogram accelerationen 1 meter per sekundtvå (newton, N),
för verkningsgrad, verkningsgraden då nyttig effekt är lika med förbrukad effekt (talet ett, 1).
För en och samma storhet kan fler än en enhet förekomma.
Exempel: 1 sekund (1 s), 1 minut (1 min), 1 timme (1 h) är olika enheter för tid.
Samma enhet kan ibland anges på skilda sätt.
Exempel: För energi är joule (J), wattsekund (Ws) och newtonmeter (Nm) olika benämningar (beteckningar) på samma enhet.
Varje särskild föremål kallas även Ett eller Enhet, då det utgör en måttstock, för att angiva antal av samma slags föremål. Sålunda utgör ett träd, ett hus m. m. enheter, till vilka man hänsyftar, då man talar om flera träd, flera hus m. m., fastän varken träd eller hus kunna anses som mätande enheter.
Mätetal
Ett mätetal anger hur många gånger den valda enheten innehålls i storheten,
ett mätetal är kvoten av storhetsvärde och enhet
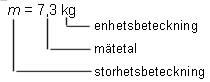
Benämnt och obenämnt tal
Antal eller tal är en förening av flera enheter, eller och av flera delar av en enhet.
Antal, som uppkommer genom upprepade sammanläggningar av en odelad enhet, kallas hela tal.
Antal, som uppkommer genom upprepade föreningar utav delar av en enhet, kallas brutna tal eller bråk.
Om man vid talets nämnande tillägger namnet på enheten, kallas talet benämnt (konkret),
t.ex.: femton meter, tre fjärdedels mil.
Om man ej tillägger namnet på enhet, eller ej fäster sig vid någon viss enhet, sägs talet vara obenämnt (abstrakt, diskret).
Med multiplikatorer i form av prefix (multipelprefix), t.ex. kilo- (k-) för faktorn 1 000, kan man i många fall bilda multipelenheter.
t.ex.: kilometer (km) och millimeter (mm) är multipelenheter till meter
| Storhet | Storhets- beteckning |
Enhet | Enhetsbenämning | Enhetsbeteckning |
| längd | l | 1 m | meter | m |
| area | A | 1 m2 | kvadratmeter | m2 |
| tid | t | 1 s | sekund | s |
| acceleration | a | 1 m/s2 | meter per sekundtvå |
m/s2 |
Teoretiskt sett kan ett mätetal vara såväl rationellt som irrationellt. Mäter man t. ex. en kvadrats diagonal med sidan som enhet kan man teoretiskt visa att diagonalens mätetal måste bli irrationellt. Sidan och diagonalen sägs därför vara inkommensurabla till skillnad från kommensurabla storheter, der den enas mätetal med den andra som enhet är rationellt.
Två sträckor är kommensurabla, om det existerar en sträcka, av vilken var och en av de givna sträckor är en multipel.
Många storheter har internationellt standardiserade beteckningar, storhetsbeteckningar. En sådan består av en stor eller liten bokstav ur vårt vanliga alfabet eller, i en del fall, ur det grekiska alfabetet. För några ovanliga speciella storheter, s.k. karakteristiska tal, består beteckningen av en stor och en liten bokstav. En storhetsbeteckning kan kompletteras med särskiljande eller kompletterande index.
Exempel:
|
|
|
Som beteckning för en speciell tillämpning av en storhet förser man den normala bokstaven med en karakteriserande indexbeteckning.
Ex. di kan beteckna inre diameter, Vmax maximal volym, f1 grundtonsfrekvens, v0 begynnelsehastighet, cp specifik värmekapacitet vid konstant tryck.
Utom de standardiserade storhets beteckningarna:
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |