| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| absolutbelopp olikhet negation |
Intervall - Olikheter |
Ekvation |
Påståendet (utsagan) som anger att två matematiska storheter är inte lika kallas olikhet.
Mellanrummet mellan två storhetsvärden kallas intervall.
Om a och b två tal på tallinjen, kallar vi mängden av alla tal som ligger mellan a och b för ett intervall.
Om a och b är två reella tal gäller antingen att a = b, att a är större än b eller a är mindre än b.
Ett intervall är en delmängd av de reella talen som bestäms av en eller två olikheter och som på tallinjen kan avbildas som en sträcka eller en halvlinje (en stråle).
Med en fylld ring markeras att en ändpunkt tillhör intervallet, och en tom ring and en ändpunkt inte tillhör intervallet.
Begränsat intervall
Intervall som på tallinjen avbildas som sträckor med eller utan ändpunkt kallas begränsade intervall:
Typer av begränsade intervall:
| Beteckning | Beskrivning | Intervallet består av alla x där: |
Bild av intervallet |
| ]a, b[ = {x |
Det öppna intervallet från a till b | a < x < b | |
| [a,b] = {x: |
Det slutna intervallet från a till b | a ≤ x ≤ b | |
| ]a,b] = {x: |
Det halvöppna intervallet från a till b | a < x ≤ b | |
| [a,b[ = {x: |
Det halvöppna intervallet från a till b | a ≤ x < b |
Punkterna a och b kallas ändpunkter. Varje punkt i det öppna intervallet ]a, b[ kallas en inre punkt till ett intervall med ändpunkterna a och b.
Obegränsat intervall
Intervall som på tallinjen avbildas som strålar med eller utan ändpunkt kallas obegränsade intervall
Typer av obegränsade intervall:
| Beteckning | Intervallet består av alla x där: |
Bild av intervallet |
| x < a | (- ∞, a) | |
| x ≤ a | (- ∞, a] | |
| x > a | (a, ∞) | |
| x ≥ a | [a, ∞) |
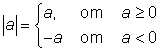
Geometriskt betyder |a| avståndet från punkten a till origo. Avståndet mellan punkterna a och b på tallinjen är |a - b| = |b - a|.
T ex är |3|=3 och |-3|=3. Det gäller, att
Om a > 0 då:
| |x| = a | betyder att | x = - a eller x = a |
| |x| < a | betyder att | - a < x < a |
| |x| ≤ a | betyder att | - a ≤ x ≤ a |
| |x| > a | betyder att | x < - a eller x > a |
Räkneregler för absolutbelopp:
|a| ≥ 0, |-a| = |a|, ![]() = |a|
= |a|
|ab| = |a|·|b|
|a²| = |a|² = a²
Triangelolikheten:
|a + b| ≤ |a| + |b|
Generellt gäller: ![]()
Omgivning
Låt d vara ett givet positivt tal. Mängden
{x: |x - a| < d}
kallas då en omgivning till a. Olika värden på d ger olika omgivningar. Om man från omgivningen ovan tar bort punkten a får man den punkterade omgivningen.
Olikhet
En olikhet är en matematisk utsaga, som säger att två matematiska storheter är inte lika stora.Olikheten A ≠ B utläses "A är inte lika med B" eller "A är skilt från B".
Olikheten A < B utläses "A är mindre än B"
Olikheten A > B utläses " A är större än B".
x ≤ 2 läses "x är mindre än eller lika med två"
En dubbelolikhet är egentligen två olikheter som skall uppfyllas samtidigt.
t.ex. 5 ≤ x ≤ 6
Negationen av en utsaga A är utsagan "icke-A" (betecknad med ¬A). Den är sann då A är falsk, falsk då A är sann. Utsagan icke-A kallas även motsatsen till A.
Motsatsen till "x = 3" är "x ≠ 3"
Motsatsen till "x < 3" är "x ≥ 3"
Räkna med olikheter
En ekvation med x som obekant satisfieras av ett eller flera skilda värden på x. En olikhet däremot gäller i allmänhet för alla värden på x i ett intervall.Mängden av de värden på obekanten för vilka en olikhet är sann kallas olikhetens lösningsmängd.
Olikhet av första graden
Förenkling av en olikhet av första graden tillgår i stort sett på samma sätt som lösning av en ekvation. Därvid gäller följande regler:
Adderar eller subtraherar vi de båda leden i en olikhet med samma tal, får vi en ekvivalent olikhet.
Multiplicerar eller dividerar vi de båda leden i en olikhet med samma positiva tal,
får vi en ekvivalent olikhet.
Två olikheter är ekvivalenta om de har samma lösningsmängd.
Multiplikation eller division med negativa tal resulterar relations ändring, olikhetstecken byter riktningen.
t.ex.
| 3 x - 1 | > | 5 | (addera 1 till båda leden) | 4 - 2 x | > | 8 | (subtrahera 4 från båda leden) |
| 3 x | > | 6 | (dividera med 3) | -2 x | > | 4 | (dividera med -2) |
| x | > | 2 | x | < | - 2 |
De värden på x, för vilka en olikhet av första graden gäller, ligger i ett intervall.
En olikhet av typen ax² + bx + c > 0 (eller < 0)
| I. | Om b ² - 4ac > 0, de värden på x, för vilka en olikhet av andra graden gäller, ligger i två (eller ett) intervall. (det indefinita fallet) |
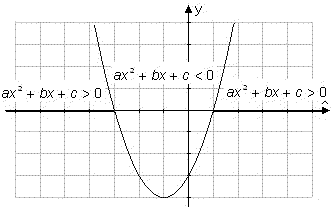 |
| II. | Om b ² - 4ac = 0, de värden på x, för olikheten av andra graden geller, alla x utom för ett x värde. (det semidefinita fallet) |
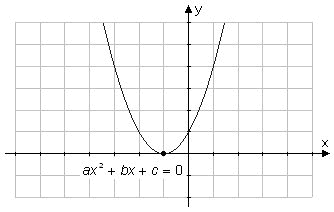 |
| III. | Om b ² - 4ac < 0, alla x-värde. (det definita fallet) |
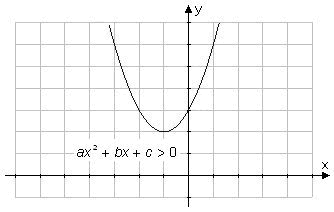 |
| a > 0 och b > 0 | medför att | a + b > 0 och a · b > 0 |
| a > b och b > c | a > c | |
| a > b och c > 0 | ac > bc | |
| a > b och c < 0 | ac < bc | |
| a > b och c > d | a + c > b + d |
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |