| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
Ekvation är en speciell framställning av ett kvantitativt problem med matematiska tecken och symboler. Syftet med ekvationen är att lösa problem, att finna obekanta storhet.
Ekvation är en matematisk utsaga (ett påstående), som säger att två matematiska storheter (eller matematiska uttryck) är lika stora.
Exemplar:
| Problem (utsaga) | Ekvation | Anm. |
| Yngve är två år äldre än Xénia. | y = x + 2 | x, y (obekanta = Yngves och Xénias ålder, de är variablarna, men oberoende på varandra.) |
| Sök fyra konsekutiva, hela udda tal, vilkas summa är 888. | x + (x + 2) + (x + 4) + (x + 6) = 888 | x (obekant, konstant = första tal) |
| Kvoten av två tal är 5/9. Talens summa är 420. | x (obekant, konstant = ena talet; andra talet är [420-x]) |
Obekanta, likhetstecken och lösning
Kännetecken för en ekvation
— en ekvation innehåller en eller flera s. k. obekanta (konstant eller variabel), som vanligen betecknade med x, y, z o.s.v.;
— en ekvation alltid har en likhetstecken i.
(Även ett uttryck med obekanta sig själv betraktas vanligen som en ekvation där uttryckets värde är lika med noll.)
t.ex.: solve(3xy - 6, x) ![]() ; solve(sin(x)+cos(x))
; solve(sin(x)+cos(x)) ![]()
däremot värdesättningen (värdetilldelningen) betraktas inte som ekvation.
(t.ex. a = 5, y(x) = x²)
En lösning (en rot) till en ekvation är ett sådant värde på den obekanta resp. sådana värden på de obekanta som innebär att likheten (mellan ekvationens bägge led) gäller.
Led
Uttrycket till vänster (eller höger) om likhetstecknet i en ekvation (eller olikhetstecknet i en olikhet) kallas ekvationens resp. olikhetens vänstra (eller högra) led (eller membrum plur. membra).
En homogen ekvation är en ekvation vars höger led är noll och vänster led är ett homogent flertermsuttryckt.
Vänstra ledet kan betecknas V L och högra ledet H L.
Ekvationslösning, satisfiering
Meningen med ekvationen är att finna det obekanta talet (lösa ekvationen). En storhet (ett tal) som, insatt i den obekantas ställe, gör en ekvations båda led alldeles lika, sägs satisfiera (gottgöra, tillfredsställa) eller uppfylla ekvationen och kallas en lösning eller ett satisfierande värde på den obekanta.
Att (upp)lösa en ekvation betyder att bestämma alla värden, som satisfiera honom, och han är upplöst, när den obekanta ensam finns på ena sidan om likhetstecknet och bara bekanta på den andra.
En ekvations lösning delas ofta i två steg: hyfsning (ordning och reducering) och den hyfsade ekvationens upplösning.
Att hyfsa menas att bringa ekvationen till enklaste form genom addition av likformiga termer och ordning av bokstavstermer alfabetiskt.
| ekvation: | 2x² - 4x - 6 | = | x² - 3x | |
| hyfsad ekvation: | x² - x - 6 | = | 0 | se "lösning av andragradsekvationer" eller WolframAlpha |
| lösning 1: x1 = -2; | 2·(-2)² - 4·(-2) - 6 | = | (-2)² - 3·(-2) | |
| lösning 2: x2 = 3 | (3)² - 4·(3) - 6 | = | (3)² - 3·(3) |
En ekvation med x som obekant satisfieras av ett eller flera skilda värden på x.
Existens av en lösning och antalet lösningar beror på bland vilka tal söker vi lösningar.
(t.ex. komplextal, reellt tal, rationellt tal, heltal).
Exempel: x² + 1 = 0 har ingen reell lösning.
För att lösa en ekvation, måste man finna alla lösningar (rötter).
Lösningsmängd
Ekvationens lösningsmängd är mängden av alla lösningar.
Ekvivalenta ekvationer
Två ekvationer är ekvivalenta om de har samma lösningsmängder.
ekvivalent = likvärdig, fullt motsvarande
t. ex. 3x + 5 = 20 ![]() x - 5 = 0
x - 5 = 0
Två ekvationer som är inte ekvivalenta är oberoende.
![]() En ekvation som kan inte härleda från andra ekvationer i en ekvationssystem kallas oberoende ekvation.
En ekvation som kan inte härleda från andra ekvationer i en ekvationssystem kallas oberoende ekvation.
Typer av ekvationer
I anseende till lösningarna kan ekvationen vara "äkta" eller indentiska eller självmotsägande.De "äkta" ekvationer (bestämnings- eller villkorsekvationer) är som riktiga för något men inte alla värden.
T.ex.: 3x + 4 = 6x - 2 (x är obekant och x = 2 är lösningen till ekvationen)
De identiska ekvationer eller identiteter är de gälla för alla möjliga värden på den obekanta.
Ibland skriver man tecknet " ≡ " för "=", för att markera en identitet.
T.ex. är 4x + 3x = 7x en identisk ekvation, den är riktig för alla möjliga värden, som för den obekanta insättas i ekvationen.
De självmotsägande (eller motstridande) ekvationer, som inte är riktiga för något värde kallas även absurditeter.
T.ex.: x + 1 = x
(a + b)(a - b) = a² - b² + 1
Algebraiska ekvationer
I anseende till formen kan ekvationer vara algebraiska eller transcendenta.
Algebraiska ekvationer är sådana, som endast innehåller summor, skillnader, produkter, kvoter, potenser och rötter av den obekanta. Lösningar till algebraiska ekvationerna kallas rötter.
Transcendenta ekvationer innehåller transcendenta (icke algebraiska) operationer av den obekanta.
Några slag är: exponentialekvationer, logaritmekvationer, trigonometriska ekvationer.
transcendent (= översinnlig, övernaturlig) = icke-algebraiskt.
Ekvationen ax³ = by är algebraisk i avseende på x, men transcendent i avseende på y.
Rationella algebraiska ekvationer
Algebraiska ekvationer kan vara rationella eller irrationella. Rationell är en ekvation, när den obekanta icke förekommer under något rottecken eller bruten (bråktals-) exponent.
Ekvationen ![]() är rationell i avseende på x, men irrationell i avseende på y.
är rationell i avseende på x, men irrationell i avseende på y.
Hyfsade rationella algebraiska ekvationer kallas även för polinomekvationer och irrationella algebraiska ekvationer kallas även för rotekvationer.
| irrationell algebraisk ekvation | (rot: x = 2) | rotekvation | |
| x + 1 = x² | rationell algebraisk ekvation | (rötter: x1 = -1, x2 = 2) | polinomekvation: x² - x - 1 = 0 |
Ekvations grader
Ekvationer innehåller en eller och flera obekanta storheter, och indelas i klasser eller grader.
En ekvation har den grad som den obekantas högsta exponent visar, eller den högsta summan av de i samma term förekommande obekanta storheternas exponenter visar.
| x - p = 0 .…(1), ax + by - c = 0. …(2) 6x + 4 = 10x - 6, 8x - 5y + 13 = 0 |
|
| x² + px + q = 0 .…(3), 10x² + 6x - 5 = 0, x² - axy + by + cx + dy + p = 0 .…(4) 3xy + 5y - 10 = 0, 4x² - 10 = 0 |
|
| x³ - px² + qx - r = 0 .…(5), 8x³ - 21 = 0, 3x²y - 5y² + 3x² - 25 = 0 |
|
| x4 - px³ + qx² + rx + s = 0 .… … (6) | Ekvation av fjärde graden |
| x n + px n-1 qx n-2 + … + K = 0 … (7) | Ekvation av n:te graden |
Ekvationerna (1), (2), (3), (4), (5), (6), (7) är hyfsade. En ekvation sägs vara hyfsad, då den obekanta inte förekommer i nämnaren, och inte är bunden av något rotmärke, då dess högsta dignitet inte har annan koefficient än 1, samt då ekvationens alla termer inte äger någon gemensam faktor, d.v.s. då en term förekommer där den obekanta inte ingår.
Ekvationen x4 + ax²y - by² - c = 0 är av 4:de graden i avseende på x men av 2:ra graden i avseende på y.
En ekvation av första graden kallas även enkel ekvation eller linjär, då en ekvation av andra graden sägs vara kvadratisk, och en av tredje graden kubisk, samt en av fjärde graden bikvadratisk.
Exempel för
den linjära ekvationen (förstagradsekvationen): 3x - 9 = 0 (rot: x = 3)
den kvadratiska ekvationen (andragradsekvationen): 2x² - 4x - 6 = 0 (rötter: x1 = -1 och x2 = 3 )*
den kubiska ekvationen (tredjegradsekvationen): x³ - 3x² - 6x + 8 = 0 (rötter: x1 = -2, x2 = 1 och x3 = 4)*
* antalet rötter motsvarar ekvationens "gradtal".
Polynomekvation
En polynomekvation är en ekvation av typen p(x) = 0, där p(x) är ett polynom.
En hyfsad ekvation av m:te graden, ordnad i avseende på x, har följande form:
x m + Ax m-1 + Bx m-2 + Cx m-3 + … + Mx + x = 0
här kan koefficienterna A, B, C, D, … inte innehålla x, men väl andra obekanta. Då i egenskap av den hyfsade ekvationens högra led är = 0, kallar man dess vänstra led ekvationens polynom.
Varje polynom kan skrivas som en produkt av polynom som alla är av första eller andra graden.
(med annat formulering: Varje algebraisk ekvation har minst en rot.)
T.ex. ![]()
Om en n:tegradsekvation har rötterna x1, x2, … xn kan den skrivas
(x - x1)(x - x2)· … ·(x - xn) = 0
Varje rot satisfierar ekvationen, vilket omedelbart framgår av att insättning ger en av parenteserna värdet 0.
Multipelrot
till en algebraisk ekvation är en rot, som förekommer mer än en gång. Dubbelrot är som förekommer två gånger, och trippelrot är som tre gånger. Om a är multipelt nollställe till polynomet p(x) sägs a vara rot av samma multiplicitet till ekvationen p(x) = a.
Diofantiska ekvationer
Ekvationer, där koefficienterna och de obekanta endast får anta heltalsvärden.
| Exempel:
En gammal räknegåta lyder så: En bonde slaktade på tre dagar sina får. Första dagen slaktade han halva antalet och ett halvt får därtill; andra dagen hälften av återstoden och ett halvt får därtill; på samma sätt tredje dagen. Hur många får hade han från början? |
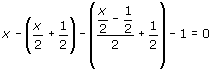 x = 7 |
I en exponentialekvation förekommer den obekanta i exponenten (t.ex. ax = b).
En
trigonometrisk ekvation innehåller trigonometriska funktioner av den obekanta (t.ex. sin(x) = 0.5).
I en differentialekvation utgörs de obekanta inte av tal utan av funktioner, närmare bestämt derivator.
Ekvationssystem i algebran, två eller flera ekvationer innehållande två eller flera obekanta; man söker de lösningar som är gemensamma för samtliga ekvationer i systemet.
Ex. 2. Skolmatematikuppgift: "Hur många skãrningspunkter har den rãta linjen y = 5x - 8 och parabeln y = (x^2)/2. Vilka ãr de eventuella skãrningspunkternas koordinater? Besvara frågorna utan att rita kurvorna."
| y = | 5x - 8 | |
| y = | x2/2 |
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |