| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| Newton-Raphson metod | Numeriska lösningar av ekvationer och olikheter |
Ekvationer Olikheter |
Iteration
Iteration är en upprepning av samma process flera gånger för att t ex förbättra noggrannheten vid en numerisk beräkning. För ett exempel, se Newton-Raphsons metod.
Intervallhalvering
Intervallhalvering innebär, som namnet antyder, att man utifrån ett givet intervall som innehåller roten evaluerar funktionen i mitten av intervallet. Tecknet på funktionsvärdet avgör vilken av ändpunkterna som ska flyttas. Genom att upprepa detta så halveras intervallet successivt och man är garanterad en rot med en viss
noggrannhet (ingenstans i intervallet är man längre än halva intervallängden från roten).
(evaluera = [ut]värdera)
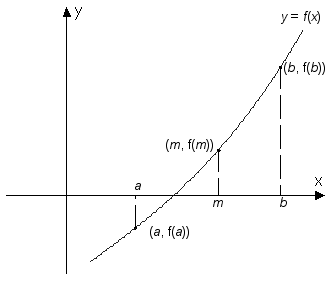 |
Vi betraktar grafen till f i intervallet a ≤ x ≤ b och antar att f(a) och f(b) har olika tecken. Om grafen är en sammanhängande kurva i intervallet så skär kurvan x-axeln på minst ett ställe i intervallet. Låt oss för enkelhetens skull anta att vi bara har en skärningspunkt och att funktionen alltså bara har ett nollställe i intervallet. Nu delar vi intervallet mitt itu och bestämmer funktionsvärdet f(m) i mittpunkten. Genom att jämföra tecknen för f(a) och f(m) kan vi avgöra på vilken sida om m skärningspunkten ligger. Därefter kan vi upprepa processen, nu med hälften så stort intervall. Denna intervallhalvering kan fortsätta tills vi stängt in vårt sökta x-värde i ett tillräckligt litet intervall. |
| a | b | m | (b-a)/2 | f(a) | f(m) |
| 1 | 2 | 1.5 | 0,5 | -1 | 2,375 |
| 1 | 1,5 | 1,25 | 0,25 | -1 | 0,453125 |
| 1 | 1,25 | 1,125 | 0,125 | -1 | -0,326171875 |
| 1,125 | 1,25 | 1,1875 | 0,0625 | -0,326171875 | 0,049560547 |
| 1,125 | 1,1875 | 1,15625 | 0,03125 | -0,326171875 | -0,141693115 |
| 1,15625 | 1,1875 | 1,171875 | 0,015625 | -0,141693115 | -0,046924591 |
| 1,171875 | 1,1875 | 1,1796875 | 0,0078125 | -0,046924591 | 0,001101971 |
Då x = 1,1796875 ± 0,0078125, med två decimaler x = 1.18
Newton-Raphson metod
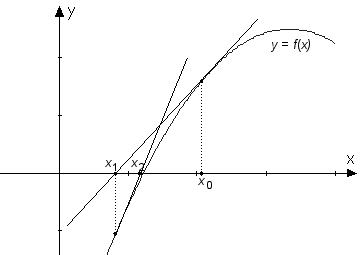 |
Metod att genom successiva approximationer bestämma närmevärden till rötterma av en ekvation f(x) = 0. Man startar med en approximation x0 av den aktuella roten. Tangenten till grafen av funktionen f i punkten (x0, f(x0)) skär x-axeln i en punkt, som betecknas x1. Denna punkt bestäms enligt formeln varvid f'(x0) är derivatvärdet av funktionen f i punkten x0. Denna process upprepas, denna gång med x1 som startpunkt, etc; allmänt bestäms xn+1 ur xn enligt formeln Under mycket allmänna villkor konvergerar följden x0, x1, x2 … mot en rot till ekvationen f(x) = 0; ett närmevärde erhålls genom att processen avbryts vid någon steg. |
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |