WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

Identitet

En identitet är i motsats till ekvation i egentlig mening en likhet, som gäller för alla tänkbara värden numeriska värden på ingående bokstavstecken. Det är en ekvation som satisfieras av alla tänkbara värden på de obekanta.

Ibland skriver man tecknet " ≡ " för "=", för att markera en identitet.

Några viktiga algebraiska identiteter om a, b och c är reella tal:

(a + b)²	=	a² + 2ab + b²	(kvadreringsreglerna)
(a - b)²	=	a² - 2ab + b²
(a + b)·(a - b)	=	a² - b²	(konjugatregeln)
(a + b + c)²	=	a² + b² + c² + 2ab + 2ac + 2bc
(a + b)³	=	a³ + 3a²b + 3ab² + b³
(a - b)³	=	a³ - 3a²b + 3ab² - b³
(a + b)n	=		binomialkoefficienter se hos kombinationer
a³ + b³	=	(a + b)·(a² - ab + b²)
a³ - b³	=	(a - b)·(a² + ab + b²)
(a + b + c)³	=	a³ + b³ + c³ + 3(a + b)(a + c)(b + c)

Tillämpningar av identiteter för uppgiftslösning

Exemplar:
1. Bestäm A och B så att
3 x = A(x - 1) + B(x + 2)

Metoden är den följande:

3 x = A(x - 1) + B(x + 2)

skall bli en identitet och skall därför gälla för alla värden på x; detta betyder att man kan införa vilka värden man vill på x utan att förstöra relationens riktighet. Lägg märke till att om man insätter x = 1 blir första termen A·0 = 0 så att man omedelbart får reda på B.

Alltså, om	x	=	1
	3	=	0 + B (1 + 2)
varav	3B	=	3
så att	B	=	1

Sätter man x = -2 blir andra termen i högra ledet noll och man finner direkt värdet på A.

Om	x	=	-2
	3(-2)	=	A (-2 - 1)+0
	-6	=	-3A
därför	A	=	2

2. Bestäm bisektrisen k i en triangel om två sidor (a, b) och den mellanliggande vinkel (γ) given. Bisektrisen delar triangeln två trianglar vars areor är: Ersätt sin γ med , förkorta med så blir ak + bk = (a + b)k = bisekritesen är k =     ( är det harmoniska medelvärdet av a och b)

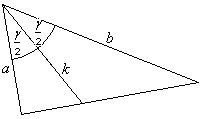Några viktiga trigonometriska identiteter

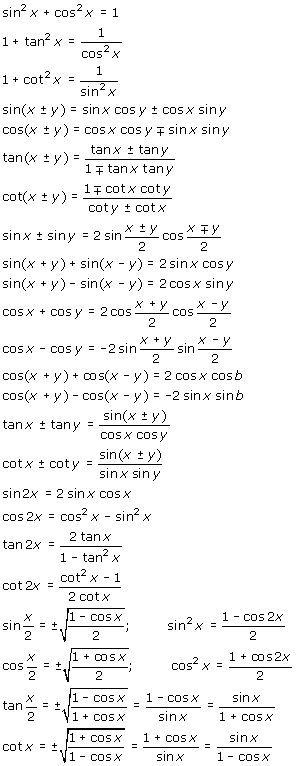
Logaritmiska identiteter

loga(m·n) = logam + logan	m, n > 0	ln(z1z2) = ln z1 + ln z2	-π < arg z1 + arg z2 ≤ π
loga = logam - logan	m, n > 0	= ln z1 - ln z2	-π < arg z1 - arg z2 ≤ π
loga k n = n·loga k	n heltal, k > 0	ln z n = n ln z	-π < n arg z ≤ π
	n heltal, k > 0	ln(-1) = πi    ln(± i) = ±½πi