WolframAlpha Lexikon Formler Terminologi länkar Svenska matematiklänkar Math. Resources on the Internet Böcker

Gästbok
Matematik minimum - Terminologi
En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik
A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö     
Klicka på någon av bokstäverna
 Nedladdning

Rätvinkliga triangel
Snedvinkliga trianglar
Liksidig triangel
Likbent triangel
Transversalsatsen
Triangel      
 Geometri - Grundbegrepp
Polygon
Triangelberäkningar
   - av rätvinkliga trianglar
   - av snedvinkliga trianglar

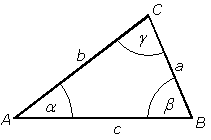
En triangel (trekant eller trehörning) är en polygon som begränsas av tre sträckor, som kallas sidor, vilkas träffpunkter kallas triangelns hörn.
Triangeln betecknas  Δ ABC, (som utläses "triangeln A B C") om hörnen kallas A, B och C.
Sidan, som står mot vinkeln α (hörnet A) betecknas vanligen med a, och kallas motstående sida till vinkeln α  (hörnet A); sidorna b och c sägs omge vinkeln α.
Vinkeln α och sidorna b och c kallas även närliggande.
De tre sidorna och de tre vinklarna kallas med ett gemensamt namn triangelns element.

Mot en större sida står en större vinkel. Mot en större vinkel står en större sida i en triangel.

Triangelolikheten
I en triangel är summan av två sidorna större än den tredje, och skillnaden mellan två sidor mindre än den tredje:

a + b > c c - a < b  
a + c > b c - b < a  
b + c > a b - a < c  
Genaraliserad med annan beteckning: |a1|-|a2| ≤ |a1 + a2| ≤ |a1|+|a2|.

Vinkelsumman i en triangel är 180º. Alltså α + β + γ = 180º.
Yttervinklarna till en triangel är tillsammans 360º. Alltså enl fig. δ + ε + ζ = 360º.

Yttervinkelsatsen:
Yttervinkeln till en vinkel i en triangel är lika med summan av triangelns andra två vinklar.

 

Med avseende på vinklarnas storlek är trianglar spetsvinkliga, om alla tre vinklarna är spetsiga rätvinkliga, om en vinkel är rät, trubbvinkliga, om en vinkel är trubbig.

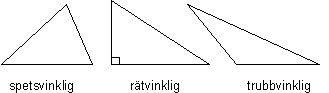
En trubbvinklig triangel är en triangel, som har en trubbig vinkel (större än 90º).
Det kan inte finnas två trubbiga vinklar i en triangel.
När en vinkel i en triangel är rätt eller trubbig, är de andra spetsiga.
En spetsvinklig triangel är en triangel, där alla vinklar är spetsiga.

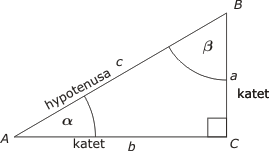
Rätvinklig triangel

En rätvinklig triangel är en triangel där en av vinklarna är rät.
De sidor, som bildar den räta vinkeln, kallas kateter och den tredje sidan, som står mot det räta vinkeln, kallas hypotenusa.

Pytagoras' sats
I en rätvinklig triangel är kvadraten på hypotenusan lika med summan av kvadraten på kateterna.
a² + b² = c²
 
När i en triangel kvadraten på en sida är lika med summan av de två andra sidornas kvadrater, är triangeln rätvinklig.

Höjdsatsen (av Euklid)

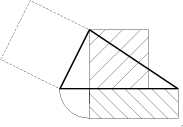I en rätvinklig triangel är kvadraten på höjden mot hypotenusan lika med den rektangel, som har hypotenusans delar till sidor.
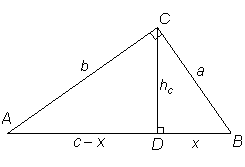I en rätvinklig triangel är höjden mot hypotenusan medelproportional till hypotenusans delar.
, varav
Höjden mot hypotenusan i en rätvinklig triangel delar den i två trianglar, som båda är likformiga med den ursprungliga triangeln.
Triangeln ACD är likformig med triangeln ABC. Förhållandet mellan trianglarnas areor är (b/c)². Likaså är trianglarna BCD och BAC likformiga, varför förhållandet mellan areorna är (a/c)². Summan av dessa förhållanden är 1, varav a²+b²=c².

Snedvinkliga trianglar

Triangeln som inte är rätvinklig kallas snedvinklig.
De snedvinkliga trianglar antingen är spetsvinkliga eller trubbvinkliga.

Med avseende på sidornas inbördes längd är trianglar liksidiga, om alla tre sidorna är lika stora likbenta, om två sidor är lika stora oliksidiga, om alla sidorna är olika stora.

.

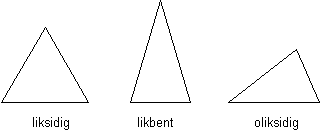
Liksidig triangel

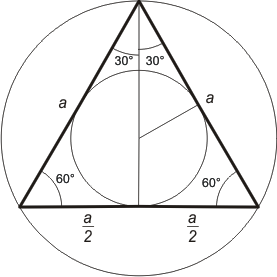
En liksidig triangel är en triangel, som har alla sidor lika stora. (Det är en regelbunden plygon.)
I en liksidig triangel är alla vinklar 60º

Följande formler gäller för en liksidig triangel med sidan a:
höjden: 
arean: 
radien för den inskrivna cirkeln: 
radien för den omskrivna cirkeln: 

Likbent triangel

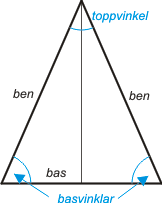
I en likbent triangel är två sidor lika stora. De lika stora sidorna kallas benen.
Den tredje sidan kallas basen.
Basens närliggande vinklar kallas basvinklar. Den tredje vinkeln kallas toppvinkel.

Basvinkelsatsen:
De två basvinklarna i en likbent triangel är lika stora.

I en likben triangel är höjden mot basen, toppvinkelns bisektris, basens mittpunktsnormal och medianen mot basen sammanfallande.

 

Likformiga trianglar

Transversalsatsen

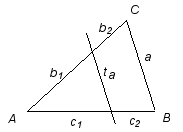
En parallelltransversal i en triagel delar de två sidorna i proportionella delar:

När en linje delar två sidor i en triangel i proportionella delar, är den en parallell transversal.

Topptriangelsatsen:

En transversal, som är parallell med en sida i en triangel, avskär en topptriangel, som är likformig med hela triangeln.
En linje, som förbinder mittpunkterna i två sidor i en triangel, är parallell med den tredje och hälften så stor som denna kallas en mittpunktstransversal.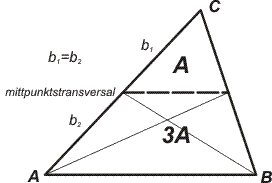

Trianglar med proportionella sidor är likformiga.

Likvinkliga trianglar är likformiga.

Likformighetsfallen

dvs. förutsättningar under vilka två trianglar är likformiga är fyra stycken:
(motsvarande sats i Euklides Elementa inom parentes).

Första likformighetsfallet (VI.6):
Om två sidor i en triangel är proportionella mot två sidor i en annan triangel och mellanliggande vinklar är lika stora, är trianglarna likformiga.

Andra likformighetsfallet (VI.5)
Om sidorna i en triangel är proportionella mot sidorna i en annan triangel, så är trianglarna likformiga.

Tredje likformighetsfallet (VI.4)
Om två vinklar i en triangel är lika stora med var sin vinkel i en annan triangel, så är trianglarna likformiga.

[Fjärde likformighetsfallet
Om två sidor i en triangel är proportionella mot två sidor i en annan triangel och den mot den större av dessa sidor stående vinkeln i den ena triangel är lika med motsvarande vinkel i den andra triangeln så är trianglarna likformiga.]

Homolog = överensstämmande, motsvarande
I fråga om ett antal kongruenta eller likformiga trianglar sägas de sidor vara homologa, som står emot lika stora vinklar, och de vinklar homologa, som står emot lika stora eller proportionella sidor.

Höjd

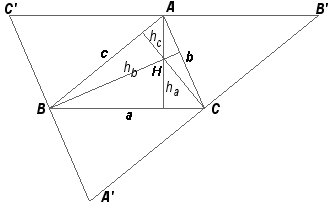
En höjd i en triangel är en linje från ett hörn vinkelrätt mot motstående sida som kallas bas.
En triangel har tre höjder, som vanligen betecknas ha, hb och hc. De skär varandra i en punkt som kallas triangelns ortocentrum.

När triangeln är spetsig, faller alla tre höjderna innanför triangeln.
Om triangeln är trubbig, faller två av höjderna utanför triangeln.
Om triangeln är rätvinklig, sammanfaller två av höjderna med kateterna.

Bisektris

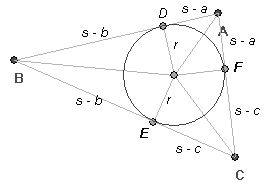
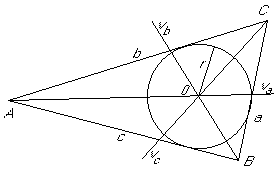
En bisektris i en triangel delar en vinkel mitt itu. Det finns tre bisektriser i en triangel, och de betecknas med vA, vB och vC.
En triangels tre bisektrisar skär varandra i en punkt, som är medelpunkt till den inskrivna cirkeln, den punkt, från vilken det är samma avstånd till alla sidor.

I varje triangel är inskrivna cirkelns radie:
(där A triangelns area, s semiperimeter, halva omkretsen, alltså s=(a+b+c)/2 )
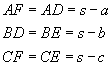
Bisektrissatsen
Bisektrisen till en vinkel delar motstående sida i två delar som förhåller sig som närliggande sidor:

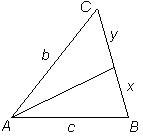Median

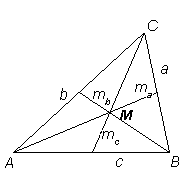
En median i en triangel är en linje från ett hörn till mittpunkten på motstående sida. Det finns tre medianer i en triangel, och de betecknas ma, mb och mc.
De tre medianer skär varandra i en punkt (triangelns tyngdpunkt).

Två medianer i en triangel skär varandra i delar som förhåller sig som 1:2. Tyngdpunktens avstånd från ett hörn i triangeln utgör sålunda 2/3 av motsvarande medians hela längd.

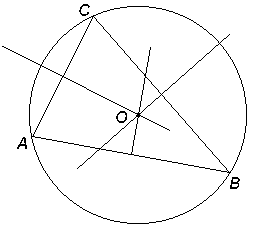
Omskriven cirkel

Den omskrivna cirkeln kring en triangel är den cirkel som går genom triangelns tre hörn; triangeln sägs vara inskriven i cirkeln. Medelpunkten O ligger i den gemensamma skärningspunkten för mittpunkstsnormalerna till triangelns sidor.
I en triangel med sidorna a, b och c är omskrivna cirkelns radie:
där A är triangelns area.

Eulers linje

I en triangel ligger höjdernas skärningspunkt H, medianernas skärningspunkt M och den omskrivna cirkelns medelpunkt O på en rät linje, som kallas Eulers linje.

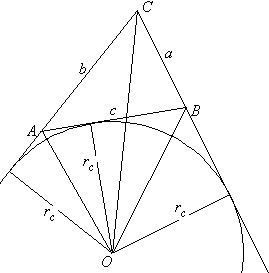
Vidskriven cirkel
En cirkel sägs vara vidskriven en triangel, om den tangerar en sida i triangeln och de båda andra sidornas förlängningar. Varje triangel har sålunda tre vidskrivna cirklar.
I en triangel med sidorna a, b och c är vidskrivna cirkelns radie:
(där A triangelns area, s halva omkretsen, alltså s=(a+b+c)/2 )

Om cirkeln tangerar sidan c och de båda andra sidornas förlängningar, betecknas dess radies längd med rc; i annat fall med ra eller rb.

Kongruensfall

Två trianglar är kongruenta, om de överensstämmer med avseende på
två sidor och mellanliggande vinkel I
de tre sidorna II
två vinklar och mellanliggande sida III
två sidor och motstående vinkel av större sidan IV

Ex. En triangel är entydigt bestämd, om man känner två sidor och en mot den större sidan stående vinkel.

av Bruno Kevius
All kopiering tillåten!   
 Matematiklexikon:
A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö
Klicka på någon av bokstäverna		    Svenska Matematiklänkar