| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| Förenkling av uttryck Faktorisering av uttryck Utveckling av uttryck Substituering av uttryck |
Uttryck |
Ekvation Formel |
Uttryck (expression)
En meningsfull sammanställning av talsymboler och tecken för räkneoperationer kallas uttryck.
| sifferuttryck | |
| bokstavsuttryck |
Ett matematiskt uttryckt innehåller siffror, bokstäver men inget likhetstecken eller andra tecken för relationer.
Uttrycket benämns vanligen efter innehållande räkneoperationer. T.ex.: algebraiskt uttryck, rationellt uttryck, bråkuttryck, potensuttryck, logaritmuttryck, rotuttryck, men additionsuttryck kallas vanligen för summa eller flertermsuttryck.
Uttrycks värde
Att beräkna ett uttrycks värde innebär att utföra de angivna räkneoperationerna och att ge resultatet i enklast möjliga form.
Förenkling av uttryck (simplifiering)
Reducering av uttrycket till en kortare form för någon vidare användning
- genom att utföra räkneoperationer och eller tillämpa matematiska identiteter,
- samt ordna bokstavsstorheter alfabetisk ordning och termerna efter fallande grad (hyfsa uttryck).
Exemplar:
| (x - 3)² + 4x² - 2x + 1 |  |
5·x² - 8·x + 10 |
| x² + 7x + 10 |  |
(x + 2)·(x + 5) |
| (a + b)·(a - b) |  |
a² - b² |
| sin²x + cos²x |  |
1 |
| 2sin(x)·cos(x) |  |
sin(2·x) |
| e2x·e5y |  |
e2·x+5·y |
Det förenklat uttryckt har ofta mindre information.
T.ex.: ![]() betyder x² och x ≠ 0
betyder x² och x ≠ 0
Det finns ingen standard matematiska regler för förenkling.
Olika symbolhanterande räknare eller programvara kan ge olika svar:
| Symplifiering med Maple: |
> expr:=2*x*(5-3*x)-2*x*(3*x-4);
|
|
| Simplifiering med Maxima: |
(%i1)
ratsimp(2*x*(5-3*x)-2*x*(3*x-4));
|
|
| Simplifiering med Mathcad: | ||
| Simplifiering med WolframAlpha |
simplify(2*x*(5-3*x)-2*x*(3*x-4))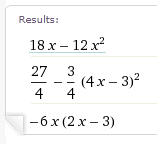
|
Faktorisering av uttryck
Omvandling av ett uttryck med flera termer till en produkt med flera faktorer för någon vidare användning.
Vanligen betyder att bryta ut gemensamma faktorer från termer.
Exemplar:
| x² + 2x |  |
x(x + 2) |
| x³ + 6x² + 11x + 6 |  |
(x + 1)(x + 2)(x + 3) |
| x3 + y3 |  |
(x + y)(x2 - xy + y2) |
| x³ + 5 |  |
(x + 51/3)·(x2 - 51/3x + 52/3) |
| 2sin(x)cos(x) + cos2(x) |  |
cos(x)(2sin(x) + cos(x)) |
Faktorisering är grundfunktion av symbolhanterande räknare eller programvaror.
T.ex. Factorisering med WolframAlpha ![]() factor(x^3+y^3+z^3)
factor(x^3+y^3+z^3)
Factoring Calculator (algebrahelp.com)
Factoring Calculator (solvemymath.com)
Factoring Calculator (freemathhelp.com)
Utveckling av uttryck
Att utveckla eller expandera av uttryck menar man att omforma produktuttrycket så att det blir summan av termer eller potensuttrycket med summan av exponent till produkt av potenser.
Exemplar:
| (x + y)2 |  |
x2 + 2xy + y2 |
| sin(x + y) |  |
sin(x)·cos(y) + cos(x)·sin(y) |
| (a + b)·(a + b2 + c) |  |
a2 + ab2 + ac + ba + b2 + bc |
| ea + ib |  |
eaeib |
| Utveckling med MuPad | 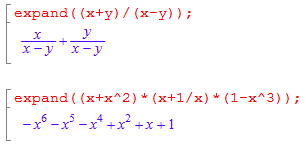 |
|
| Utveckling med WolframAlpha |
expand((x^2-2*x)*(x-1)) |
Substituering av uttryck
Substituering kallas insättning ett uttryck eller en storhet i ett annat uttryck. Förfarandet används vanligen vid lösning av ekvation, ekvationssystem, evaluering av integraler.
Till exempel:
| ersätta | i | ger |
| x = 3y | 2x - 4y = k | 2y = k |
| x = sin t |
De symbolhanterande räknare och programvaror kan substituera t.ex.:
| Substituering med Maxima: | 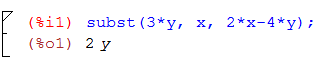 |
| Substituering med Mathcad: | |
| Substituering med Maple: | 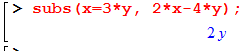 |
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |