WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

Bråkuttryck - en betecknad division

Bråk är ett uttryck av formen ,     a kallas täljare, b nämnare. Strecket kallas bråkstreck.

När missförstånd inte befaras, kan snett bråkstreck (/) användas. (a/b, 2/3)

Ett bråk är icke annat än en betecknad division, där täljaren motsvarar dividenden och nämnaren motsvarar divisorn.
 
Nämnaren (b) får aldrig vara noll.

Dubbelbråk
Ett bråk i vilket både täljare och nämnare i sin tur utgörs av bråk. Följande allmänna regel gäller:

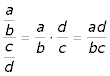
Liknämniga bråk
Bråk, vilkas nämnare är lika, t. ex. bråken kallas liknämniga bråk. Endast sådana bråk kunna omedelbart adderas och subtraheras. Andra bråk måste dessförinnan göras liknämniga, vilket sker genom bråkens "förlängning". Denna operation kallas i äldre matematiska arbeten i som isomeri.

Räkneregler för bråk

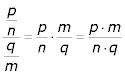
Exempel

Förkorta bråk, förlänga bråk
Om man multiplicerar eller dividerar ett bråks täljare och nämnare med samma tal (som inte är noll) får man ett nytt bråk, som betecknar samma tal som det ursprungliga bråket. Detta förfaringssätt kallas att förlänga resp. förkorta bråket.
   (förlängt med 3)
(förkortat med 5)

Bråktal (brutet tal)

Rationella tal som är icke heltal kallas för bråk (bråktal).

Bråktal är en del eller en förening av flera lika stora delar av en enhet.

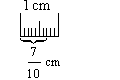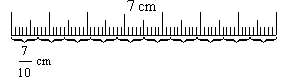Skrivsättet kan tolkas två sätt:
1) Vi har delat talet 1 i 10 lika delar och tagit 7 av dessa. Vi får bråket
2) Bråkstrecket är ett divisionstecken, och talet kan därför ges betydelsen av att vi delat talet 7 i 10 lika delar. Av figuren framgår, att talet är lika stort i båda fallen.

Ett bråktal utläses "m n-tedelar". Alltså är ²/₃ två tredjedelar, ⁷³/₂₅₆ är sjuttiotre tvåhundrafemtiosjättedelar och 3 ⁷/₁₇ är tre och sju sjuttondelar

Man skiljer allmänna bråk från decimalbråk.
(De äldre termerna "allmänt bråk" och "decimalbråk" används inte numera)

Allmänt bråk

Allmänt bråk (rationellt tal i bråkform) är ett bråk, vars täljare och nämnare är heltal.

• Äkta eller egentliga bråk: nämnaren är större än täljaren. Om täljaren är ett (t.ex. ¹/₅) kallas bråket stambråk.
• Oäkta eller oegentliga bråk: täljare är större än nämnaren. (t.ex. ²²/₇). Ett oäkta bråk kan man genom att utföra divisionen dela upp i ett heltal och ett äkta bråk (3 + ¹/₇) (se blandad form).

Decimalbråk

Ett decimalbråk är ett bråk, vars nämnare är ett dekadiskt tal, dvs. som skrivs med en etta följd av en eller flera nollor, t.ex. 10, 100, 1000 osv.

Ett decimalbråk kan skrivas , men vanligtvis skriver man endast täljaren och anger nämnarens värde genom ett komma, s.k. decimalkomma (decimaltecken), på så sätt att till höger om kommatecknet skrivs lika många siffror, som man har nollor i nämnaren.
(decimaltecken är utomlands ofta en punkt)
Bråken skrivs enligt denna regel i decimalform: 0,7; 0,04; 0,032.
Siffror till höger om kommatecknet motsvarar täljaren och kallas decimaler.

Ett avslutat decimalbråk (ändligt decimalbråk) kan skrivas som allmänt bråk genom att man skriver decimalerna som täljare och som nämnare en etta följd av lika många nollor som antalet decimaler. Bråket förkortas som möjligt.
Exempel:

Decimalutveckling

Det rationella talet har decimalutvecklingen 0,432 432 4 …, som är periodisk.
För att visa periodiciteten är en punkt placerad över den första och sista siffran i (eller en sträcka över) den grupp som repeteras.
Alltså = 0,142857 = 0,142857142857142...
Irrationella tal har icke-periodiska decimalutvecklingar.

Varje ändligt decimalbråk är ett rationellt tal, men vissa rationella tal kan inte skrivas som ändliga decimalbråk. Varje rationellt tal kan skrivas som en oändligt decimalbråk. Det gäller att ett decimalbråk till ett rationellt tal alltid blir periodiskt i den meningen att samma ändliga sifferkombination återkommer gång på gång från och med en viss punkt i decimalutvecklingen.

Även periodiska decimalbråk kan förvandlas till allmänna bråk. I täljaren skrivs siffrorna t.o.m. första perioden minus siffrorna före perioden. I nämnaren skrivs så många nior, som det finns siffror i perioden, följd av så många nollor, som det finns siffror före perioden (men efter decimalkommat).
Exempel: