| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
Partialbråk - partialbråksuppdelning
Partialbråksuppdelning av rationella uttryck
I många sammanhang har man behov av att kunna skriva ett rationellt uttryck (en kvot mellan två polynom) som en summa av enklare rationella uttryckt, s. k. partialbråk. Nedanstående uttryck är ett exempel på en uppdelning i partialbråk
![]()
En partialbråksuppdelning av ett rationellt uttryck i reella partialbråk är alltid möjlig om nämnarens gradtal år högre än täljarens gradtal samt om dessutom nämnaren kan upplösas i sinsemellan olika reella faktorer.
Metoden med obestämda koefficienter
Exempel 1.Uppdela i partialbråkExempel 2
Lösning
En uppdelning av detta i partialbråk sker genom att vi sätterBringa bråket i högra ledet på gemensam nämnare!där A och B är konstanter.
Betrakta nu uttrycken i täljaren i de båda leden. För att uttrycken skall vara lika, så måste vi kräva att de två förstagradspolynomen
5x + 7skall vara identiska. Följaktligen skall dels koefficienten för x och dels den konstanta termen i förstagradspolynomen vara lika. Alltså gäller
och
A(x + 2) + B(x + 1) = (A + B)x + (2A + B)
Lösningen till ekvationssystemet blir
A = 2 och B = 3Den sökta partialbråksuppdelningen är följaktligen
Uppdela i partialbråkEftersom nämnarens gradtal är högre än täljarens gradtal och dessutom nämnaren består av reella faktorer, så kan det givna uttrycket uppdelas i partialbråk. Antalet partialbråk är lika med antalet faktorer i nämnaren.Bringa bråket i högra ledet under gemensamt bråkstreck. Då erhållesBringa täljaren i högra ledet, så att detta andragradspolynom kommer under den allmänna formen. Då erhållesFör att ovanstående likhet skall gälla, så måsteLösningen till ovanstående ekvationssystem med tre obekanta ärA = 2, B = 1 och C = -1.Alltså är
En elegantare metod för bestämning av koefficienterna är följande: Betrakta det uttryck som gavs i det föregående exemplet:
1. Multiplicera båda leden med den första faktorn (x + 1). Då erhållesSätt x = -1, så att faktorn (x + 1) blir lika med noll! Då erhålles2. Multiplicera båda leden med den andra faktorn (x - 1). Då erhålles, A = 2
Sätt x = 1, så att faktorn (x - 1) blir lika med noll! Då erhålles3. Multiplicera båda leden med den tredje faktorn (x + 2). Då erhålles, B = 1
Sätt x = - 2, så att faktorn (x + 2) blir lika med noll! Då erhålles, C = -1
Partialbråksuppdelning med Maple:
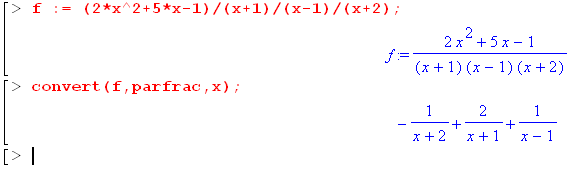
Partialbråksuppdelning med Mathematica:
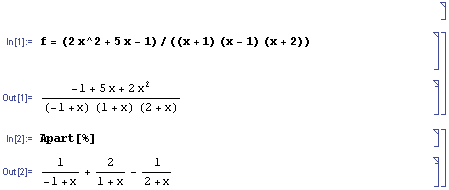
Partialbråksuppdelning med Maxima:
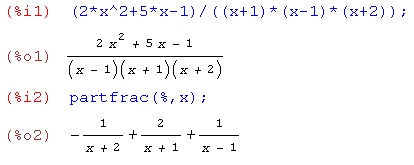
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |