Derivata - Matematik minimum - Terminologi och begreppsförklaring

Matematik minimum - Terminologi
En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik
A B C D E F G H I J K L M N O P Q R S T U V X Y Z Å Ä Ö
Klicka på någon av bokstäverna

Nedladdning

Medelvärdessatsen
Taylors formel
Differential
Derivering
Derivative Calculator

Derivata - Derivering

Analys
Derivator
Gränsvärde

Derivatan är ett mått på hur snabbt en storhet (beroende variabeln) ändras då man varierar en annan storhet som den är beroende av.

Derivatan av en funktion anger dess förändringshastighet.

En funktion (ƒ) ändrar sitt värde (ƒ(x)), då x förändras.
Derivatan av en funktion (ƒ’) anger hur funktionens värde (ƒ(x)) varierar när värdet på x förändras.

Beteckning:
Med ƒ(x) betecknas även funktionen ƒ och med ƒ’(x) dess derivata om man vill betona att oberoende variabel är x och deriveringen görs med avseende på x.

Differenskvot

Uttryck som , och kallar vi allmänt differenskvoten.
(ändringen av funktionsvärdet (beroende variabeln) dividerat med ändringen av oberoende variabeln)

Deriverbarhet och geometrisk betydelse

En funktion sägs vara deriverbar eller differentierbar om ett dylikt gränsvärde existerar.
Om (differens)kvoten närmar sig ett bestämt värde då x → x₀, sägs ƒ(x) vara deriverbar för x = x₀.

Detta är förhållandet om funktionen är kontinuerlig och saknar spetsar. Är däremot funktionen diskontinuerlig eller har en spets för ett visst x-värde, kan derivatans värde för detta x-värde bli olika allt eftersom Δx < 0 eller Δx > 0 (och derivatan har således icke då något bestämt värde för ifrågavarande x-värde).

Att en funktion ƒ(x) är deriverbar för x = x₀ betyder geometriskt, att grafen till ƒ(x) har en tangent i punkten (x₀ , ƒ(x₀)). Derivatvärdet ƒ’(x₀) är riktningskoefficienten för denna tangent och anger därmed lutningen hos kurvan.

Derivatan av funktionen ƒ med avseende på x (derivatan av ƒ(x))^{[* se beteckning]}

Om y = ƒ(x) är kontinuerlig i ett intervall (a,b) och deriverbar för varje x mellan a och b, definieras genom gränsvärdet

en funktion av x som benämns derivatan av ƒ(x). Den betecknas ƒ’(x) och utläses "f prim x".

Δy och Δx benämns de ifrågavarande variablernas tillskott (inkrement).
utläses "limes för Δy genom Δx, då Δx går mot noll"

Derivatan av en funktion beräknas genom derivering av funktionen.

Se derivator/deriveringsformler av elementära funktioner

Exempel:

Beteckningar för derivatan

Om funktionen är framställd på formen används någon av följande beteckningar:

	(efter Leibniz)
	(efter Newton)
ƒ’(x), y’	(efter Lagrange)
Dƒ(x), Dy, D_xy	(efter Arbogast, Cauchy)

Beteckningen utläses "de-y-de-ex"; inte "dy genom dx"

Som symbol för operationen derivering används D eller .

Derivator av högre ordning

Om derivatan ƒ’ till en funktion är deriverbar, kallas dess derivata andraderivatan till ƒ. Man skriver ƒ’’ eller D²f(x) eller eller .
Beteckningen ƒ’’ utläses "f biss" och beteckningen utläses "d två y d x två".

På motsvarande sätt definieras tredje derivatan ƒ’’’ som derivatan av ƒ’’ och allmän n:te derivatan ƒ⁽ⁿ⁾ som derivatan av ƒ^(n-1).

Rolles sats

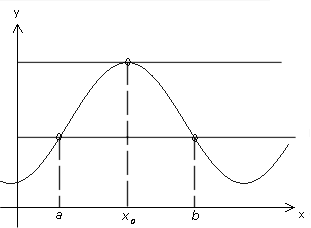Figuren visar den grafiska bilden av en funktion ƒ(x), som är kontinuerlig och deriverbar inom intervallet a ≤ x ≤ b. Vidare gäller att

ƒ(a) = ƒ(b)

Den följande satsen grundar sig på den iakttagelsen att det måste finnas minst en punkt x₀ mellan x = a och x = b i vilken kurvan har en horisontell tangent.

Rolles sats: Om funktionen ƒ(x) är kontinuerlig och har kontinuerlig derivata inom intervallet a ≤ x ≤ b och om ƒ(a) = ƒ(b), så finns det minst ett värde x, mellan a och b, sådant att

ƒ’(x) = 0

Medelvärdessatsen

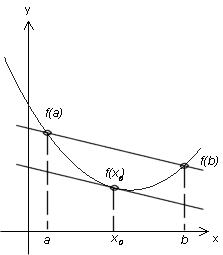Om funktionen ƒ(x) är kontinuerlig och har kontinuerlig derivata inom intervallet a ≤ x ≤ b, så finns det åtminstone ett värde x, mellan a och b för vilket gäller

ƒ(b) -ƒ(a) = (b - a)ƒ’(x₀)

där ƒ’(x₀) betecknar derivatan av ƒ(x) med insatt värde x = x₀, dvs. derivatan i punkten x₀.

Om vi låter b vara en löpande x-koordinat kan medelvärdessatsen även skrivas

ƒ(x) = ƒ(a) + (x - a)ƒ’(x₀)

där talet x, måste vara beläget i intervallet mellan a och x.

Det finns en generalisering av medelvärdessatsen, som brukar kallas Cauchys medelvärdessats. Den säger att om ƒ och g är kontinuerliga i det slutna och begränsade intervallet [a, b] och deriverbara i ]a, b[, samt om g(a) ≠ g(b) och g’ är skild från noll i ]a, b[, så finns det minst en punkt x₀ i ]a, b[ sådan att

Taylors formel

Antag att ƒ(x) är en deriverbar funktion och att vi önskar uppskatta ƒ(x) för värden på x, som ligger nära ett visst värde a. Med hjälp av medelvärdessatsen erhålls

ƒ(x) - ƒ(a) = (x - a)ƒ’(x₀), varav

ƒ(x) = ƒ(a) + (x - a)ƒ’(x₀)

där x₀ är ett tal beläget i intervallet mellan a och x.

Om ƒ(x) är deriverbar n gånger kan konstanten ƒ(a) i ekvationen ersättas med ett polynom av graden n - 1. Då erhålles en bättre approximation av ƒ(x) för värden på x, som ligger nära det fixa värdet a.
Ovannämnda generalisering av ekvationen kallas Taylors formel: Om funktionen ƒ(x) och dess n första derivator är kontinuerliga i det slutna intervallet från a till x, gäller

där R_n(x) är den s. k. resttermen, vilken kan uppskattas med formeln

den s. k. Lagranges restterm.

I det fall resttermen

R_n(x) → O då n → ∞

erhålles den konvergenta oändliga serien

som brukar kallas Taylors serie.

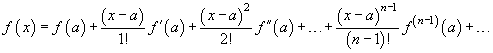
MacLaurins utveckling

Om vi i Taylors formel sätter a = 0 erhålles MacLaurins formel:
Om funktionen ƒ(x) och dess n första derivator är kontinuerliga i det slutna intervallet från a till x gäller

där resttermen uppskattas med hjälp av formeln

där 0 < θ < 1

I det fall resttermen

R_n(x) → O då n → ∞

erhålles den konvergenta oändliga serien

(se WolframAlpha:

)

som brukar kallas Mac-Laurin serie.

Utvecklingen av ƒ(x) = e^x

Då funktionen ƒ(x) = e^x är kontinuerlig för alla x och denna funktions alla derivator är lika med funktionen själv, dvs. ƒ⁽ⁿ⁾(x) = e^x inses omedelbart att funktionens samtliga derivator är kontinuerliga för alla x.
Funktionen kan alltså utvecklas enligt MacLaurins formel. Vi får ƒ(0) = e⁰ = 1 och även ƒ⁽ⁿ⁾(0) = e⁰ = 1
Således blir MacLaurinutvecklingen av
() där R_n(x)→0 då n→∞
vilken ekvation gäller för alla x.

Utvecklingen av sin x och cos x

Funktionen ƒ(x) = sin(x) och tillhörande derivator är kontinuerliga för alla x.

ƒ(x) = sin x ƒ(0) = sin 0 = 0

ƒ’(x) = cos x ƒ’(0) = cos 0 = 1

ƒ’’(x) = - sin x ƒ’’(0) = - sin 0 = 0

ƒ’’’(x) = - cos x ƒ’’’(0) = - cos 0 = -1

ƒ⁽⁴⁾(x) = sin x ƒ⁽⁴⁾(0) = sin 0 = 0

ƒ⁽⁵⁾(x) = cos x ƒ⁽⁵⁾(0) = cos 0 = 1

I MacLaurinutvecklingen erhålles
() där R_n(x)→0 då n→∞
Om vi på motsvarande sätt utvecklar ƒ(x) = cos x enligt MacLaurins formel, så erhålles
() där R_m(x)→0 då m→∞

Differential

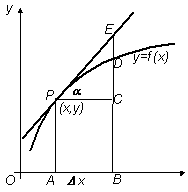Om en funktion y = ƒ(x) abskissan x för punkten P undergår förändring PC = Δx, får ordinatan y utefter kurvan förändringen CD = Δy (funktionens ändring). Samtidigt ändras ordinatan y utefter tangenten PE genom P med beloppet CE. Denna senare förändring tecknas dy och benämns funktionens differential. Man har emedan tan α = ƒ ’.

Storheten Δx, som betyder en godtycklig förändring hos x, skrivs i detta sammanhang dx och benämns den oberoende variabelns differential. Man har alltså, att

Differentialen dy kan uppfattas som det tillskott utefter tangenten, som motsvarar tillskottet dx i den oberoende variabeln x. Om dx är ett litet tal, så kommer dy att nära motsvara tillskottet Δy i variabeln y. Under denna förutsättning gäller alltså approximativt

Om dx är en icke försumbart liten storhet dx = h, så gäller

Ovanstående serie framgår genom en utveckling av ƒ(x+h)-ƒ(x) i en Taylors serie.

Derivering

är den operation som överför en funktion i sin derivata.

Länk: Derivative Calculator

Om ƒ och g är deriverbara funktioner och a är ett reellt tal så är även funktionerna a·f, ƒ + g, och ƒ·g deriverbara och följande regler gäller:

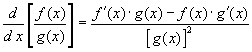
I ett intervall där g(x) ≠ 0 är även f/g deriverbar och

Exemplar:

()
()
()

Derivering av en sammansatt funktion

Länk: Derivative Calculator

För en sammansatt funktion gäller den s k kedjeregeln.
För att derivera i avseende på x en funktion, sådan som y = ƒ(z), där z betyder en funktion av x, beräknar man först derivatan

, såsom om z vore den oberoende variabeln, och multiplicerar sedan denna med derivatan av z, tagen i avseende på x.

y(x) = ƒ[g(x)] y(z) = ƒ(z), z(x) = g(x)
y’(x) = ƒ’[g(x)]·g’(x) eller

Exempel på derivatan av en sammansatt funktion (inre derivatan)

y = sin u, där u = x²,

så är

y = sin x²

en sammansatt funktion av den oberoende variabeln x. Då x får ett tillskott Δx, så får u ett motsvarande tillskott Δu och y ett motsvarande tillskott Δy. Då Δx→0, så gäller även Δu→0 och Δy→0. Man har

eller, om gränsövergång görs, varvid Δx→0,

Här är

den sammansatta funktionens derivata med avseende på den oberoende variabeln x och

den derivata, som erhålls, om man i funktionen sin u betraktar u, som om u vore oberoende variabel.
Sålunda är

(brukar kallas den "inre derivatan")

varav

eller

Några exemplar till:
(se WolframAlpha: )
(se WolframAlpha: )

Derivering av funktioner i implicit form
Implicit derivering

En funktion där y inte är löst kallas implicit. Den kan skrivas i formen F(x, y) = 0, är

Exempel:

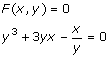
Derivering sker på vanligt sätt, under beaktande av att derivatan av y är y ’ och derivatan av x är 1

varur
Med Maple 12 (symbolhanterande programvara)

Derivering av funktion i parameterform

Funktioner i parameterform:

x = φ(t) y = ψ(t)

Logaritmisk derivering

Exempel. Derivera y = x^{sin x} ()
För att derivera en sådan funktion logaritmerar man funktionen, varefter derivering är möjlig.

av Bruno Kevius
All kopiering tillåten!

Matematiklexikon:
A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö
Klicka på någon av bokstäverna

Svenska Matematiklänkar

ƒ(x) = sin x	ƒ(0) = sin 0 = 0
ƒ’(x) = cos x	ƒ’(0) = cos 0 = 1
ƒ’’(x) = - sin x	ƒ’’(0) = - sin 0 = 0
ƒ’’’(x) = - cos x	ƒ’’’(0) = - cos 0 = -1
ƒ⁽⁴⁾(x) = sin x	ƒ⁽⁴⁾(0) = sin 0 = 0
ƒ⁽⁵⁾(x) = cos x	ƒ⁽⁵⁾(0) = cos 0 = 1