WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

Om en variabel x successivt antar värden, som allt mer och mer närma sig en viss konstant a, och det så, att skillnaden mellan a och x kan göras numeriskt mindre än vilken storhet man än må uppge, så sägs x närma sig eller tendera obegränsat (indefinit) mot a, och a kallas vara limes eller gränsvärde för x.
Detta förhållande tecknas så: lim x = a.

Gränsvärden av en talföljd

| a_n - A | < ε för alla naturliga tal n sådana att n > ω

Talföljden a_n, n = 1, 2, 3, …, sägs då också vara konvergent (med gränsvärdet A), eller sägs konvergera mot A, då n går mot oändligheten.

a_n → A, då n → ∞ eller .

(utläses: limes för a_n då n går mot oändligheten är A.)

Räkneregler för gränsvärden

Om och , så gäller

1. (α och β konstanter)
2. 
3. Om B  ≠ 0 så
4. Om a_n ≤ b_n för alla n > något n₀, så är A ≤ B.
5. Om A = B och vidare talföljden c_n, är sådan, att a_n≤ c_n≤ b_n för alla n>n₀ så .

Gränsvärden av en funktion

= A

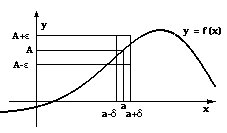En funktion sägs ha gränsvärdet  A  i punkten  a,  om det till varje positivt tal  ε  hör ett positivt tal  δ  sådant att |ƒ(x) - A| < ε,  om 0 < |x - a| < δ. Detta kan skrivas ƒ(x) → A då x → a och utläsas "fx går mot A då x går mot a". Gränsvärdet betecknas , vilket utläses "limes för fx då x går mot a".  = B   betyder, att det till varje positivt tal  ε  hör ett positivt tal  N  sådant att |ƒ(x) - B| < ε,  om |x| > N.

Exemplar på gränsvärden		Beräkningar med WolframAlpha:
		limit(sin(x)/x,x->0)
		limit(a^n/n!,n->inf)
		limit((1+z/x)^x,x->inf)

Höger- och vänstergränsvärden

Funktionen ƒ(x) sägs ha högergränsvärdet A, då x går mot a, om till varje ε > 0 finns ett δ > 0, så att
|ƒ(x) - A| < ε  för alla x sådana att a < x < a + δ.

Funktionen ƒ(x) sägs ha vänstergränsvärdet A, då x går mot a, om till varje ε > 0 finns ett δ > 0, så att
|ƒ(x) - A| < ε för alla x sådana att a - δ < x < a.

Detta kan skrivas:
ƒ(x) → A då x → a+ (högergränsvärde)
ƒ(x) → A då x → a- (vänstergränsvärde)
och utläsas "fx går mot A då x går mot a från höger (vänster)."
Gränsvärdena betecknas resp .

Funktionen ƒ är definierad i en punkterad omgivning av x = a. Ett nödvändigt och tillräckligt villkor för att existerar är att och existerar och är lika.

Räkneregler för gränsvärden.

Om och så gäller

1. 
2. 
3. Om B ≠ 0 så
4. Om ƒ(x) ≤ g(x) i någon punkterad omgivning av a, så är A ≤ B.
5. Om A = B och vidare funktionen h är sådan att f(x) ≤ h(x) ≤ g(x) i något punkterad omgivning av a, så .

Exemplar:

l'Hospitals regel

En enkel regel för bestämning av funktioners gränsvärden, då dessa antar en obestämd form, kan erhållas med hjälp av medelvärdessatsen.
Betrakta uttrycket

där ƒ(a) = g(a) = 0
Eftersom ƒ(a) = 0 och g(a) = 0, så gäller

Med hjälp av medelvärdessatsen erhålls
och
där x₁ och x₂ är belägna inom intervallet mellan x och a. Vi får alltså

Om vi låter x → a, så går både x₁ och x₂ mot a, eftersom båda är belägna inom intervallet mellan x och a.

Om ƒ och g är definierade och deriverbara med g'(x) ≠ 0 i en punkterad omgivning av x = a samt om ƒ(x) och g(x) → 0, då x → a, så gäller det att
    om det gränsvärdet existerar.

Skulle kvoten ƒ'(x)/g'(x) också vara obestämd, kan man upprepa tillvägagångssättet, och undersöka, huruvida uttrycket ƒ''(x)/g''(x) har något gränsvärde.

Exemplar

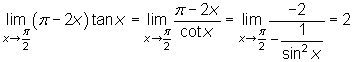
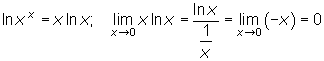
Kontinuitet

En funktion ƒ(x) är kontinuerlig för x = a om

ƒ(x) är definierad för x = a,

ƒ(x) har ett gränsvärde då x går mot a,

detta gränsvärde är lika med ƒ(a).    

( = ƒ(a))

En funktion, y=ƒ(x) är kontinuerlig för x=a, om den för detta x-värde har ett ändligt och fullt bestämt värde, och om vidare ƒ(a+δ) tenderar obegränsat mot ƒ(a), under det δ tenderar mot noll.

Funktionen ƒ(x) sägs vara kontinuerlig i ett intervall om den är kontinuerlig i varje x i intervallet.

Om en funktion är kontinuerlig i sitt definitionsområde kallas för korthetens skull en kontinuerlig funktion.

Om funktionen ƒ(x) inte är kontinuerlig för x = a sägs ƒ(x) ha en diskontinuitet för x = a.

Begränsade talmängder

En talmängd M är begränsad uppåt om det finns ett tal B, sådant att
x ≤ B   för alla x M.
Talet B kallas en majorant till mängden M.

Talmängden M är begränsad nedåt om det finns ett tal b, sådant att
x ≥ b   för alla x  M.     
Talet b kallas en minorant till mängden M.

Talmängden M är begränsad om den är både uppåt och nedåt begränsad.

Supremumaxiomet
Varje icke-tom talmängd M som är uppåt begränsad har en minsta majorant.

Den minsta majoranten till en talmängd M kallas supremum M och skrivs sup M.

Den största minoranten till en talmängd M kallas infimum M och skrivs inf M.