| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| Riktningskoefficient k-form Tvåpunktsform |
Den räta linjens ekvation
|
Ekvation Algebraiska ekvationslösningar Koordinatsystem i planet |
I den analytiska geometrin i planet studeras linjer i ett koordinatsystem.
Allmän (kanonisk) form av förstagradsekvation med två obekanta:
Ekvationen Ax + By + C = 0 är en förstagradsekvation med två obekanta (x, y) och representerar en rätt linje.
Den linjära ekvationen Ax + By + C = 0 satistifieras av oändligt många (tal)par (x, y); tillsammans utgör dessa en rät linje (grafen för denna ekvation).
Och därtill även y är en funktion av x eller x är en funktion av y.
![]() (B ≠ 0) eller
(B ≠ 0) eller ![]() (A ≠ 0)
(A ≠ 0)
Avskärningsform eller interceptform
| för räta linjens ekvation är | ||
| där a är x-koordinaten för linjens skärningspunkt med x-axeln och b y-koordinaten för linjens skärningspunkt med y-axeln. 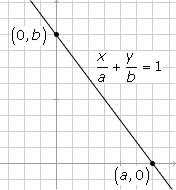
|
I planet är x-interceptet och y-interceptet för grafen till en ekvation dess skärningspunkter med x-axeln respektive y-axeln; intercepten erhålls genom att man sätter den ena variabeln lika med noll och beräknar den andra.
Exempel: 3x + 4y - 12 = 0 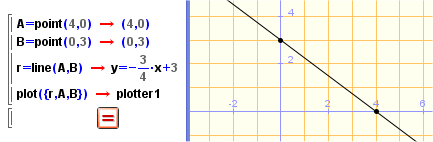
|
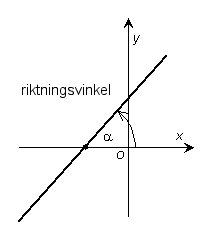
Riktningsvinkel Riktningen av en linje anges av des riktningsvinkel, som är vinkeln (tagen moturs) mellan positiva x-axeln och linjen.Riktningsvinklarna ligger mellan 0º och 180º. |
 |
|
Riktningskoefficient Riktningskoefficienten (vinkelkoefficienten) för en rät linje definieras som
|
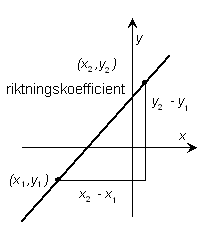 |
| Med en annan formulering är riktningskoefficienten den ordinata ökning, som svarar mot en abskissa ökning på ett. | 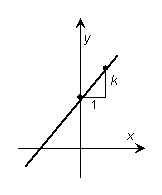 |
Linjer parallella med x-axeln har noll riktningskoefficient. Linjer som parallella med y-axeln har riktningskoefficienten ± ∞ Två parallella linjer har samma riktningskoefficient. När två linjer har samma riktningskoefficient, är linjerna parallella. När två linjer är vinkelräta, är produkten av deras riktningskoefficienter lika med -1. α = α1 + 90º |
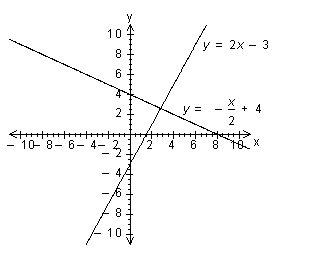 |
Vinkel α mellan två räta linjer, vilkas vinkelkoefficeinter är k1 och k2, erhålles ur ekvationen:
![]()
|
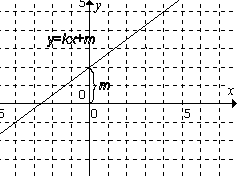
k-form Räta linjens ekvation i k-form är y = k x + m.där k = riktningskoefficienten,m = linjens avskärning på y-axeln utanför svenska skolor är vanliga formen: y = mx + b |
 |
Enpunktsform
Formeny - y1 = k(x - x1)
där (x1,y1) är en punkt på linjen och k är riktningskoefficient, kallas enpunktsformen för räta linjens ekvation.Tvåpunktsformen
för räta linjens ekvation är![]() ,
,
Exempel: Bestäm ekvationen för den räta linje som går genom punkterna (0, 3) och (4, 9).
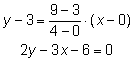
Parameterformen
för räta linjens ekvation ärNormalform
I planet är normalformen för ekvationen för en rät linje följande:
x cos Θ + y sin Θ - p = 0p är vinkelräta avståndet från origo till linjen, |
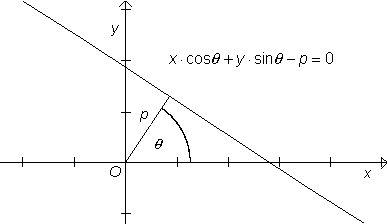
|
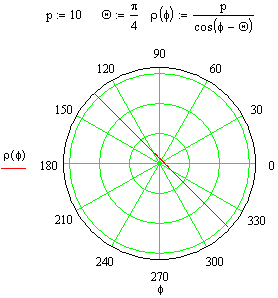
| Räta linjes ekvation i polära koordinatsystem
p är vinkelräta avståndet från origo till linjen, |
 |
Avståndsformler
Avståndet mellan två punkter (x1,y1) och (x2,y2) är:![]()
Mittpunktsformeln
Om M(x0,y0) är mittpunkten på en sträcka, vars ändpunkter är A (x1,y1) och B (x2,y2) gäller formlerna
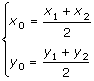
Tyngdpunktsformeln
Om en triangelns hörn har koordinaterna (x1, y1), (x2, y2) och (x3, y3) är tyngdpunktens koordinater
![]()
Delningsformeln
| Om M (x0,y0) delar AB i figur i förhållandet m:n, får vi enligt transversalsatsen AD:DC = m:n, varav Därur fås 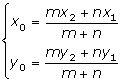 |
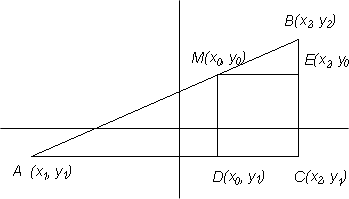 |
Areaformeln (Ytformeln)
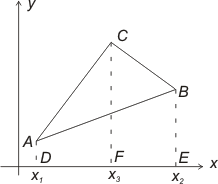
| En triangel har sina hörn i punkterna A(x1,y1), B(x2,y2) och C(x3,y3). Arean av ΔABC får om vi drar arean av ABED trapets från summan av areor av ACFD och BCFE trapetser.
|
 |
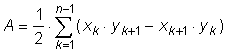
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |