| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
Matriser
Matris (Matrix) i matematiken är ett rektangulärt schema av tal, storheter eller funktioner, vilka kallas matrisens element och på vilket vissa räkneregler tillämpas. De vågräta raderna i en matris kallas rader, de lodräta kolonner (kolumner).
Ett tal i en matris betecknas Aij, där indexet entydigt anger talets plats i matrisen, i raden och j kolonnen. En matris med m rader och n kolonner benämns en m×n-matris (eller en matris av ordning m×n).
Större parentestecken används för att markera matriser. Hakparenteser förekommer också.
Exempel: Matriser
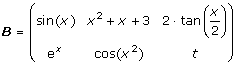
har två rader och tre kolonner och sägs därför vara 2 × 3 matriser och elementen a23 = 5, resp. elementen b11 = sin(x).
En matris med lika många rader som kolonner kallas kvadratisk matris, t ex:
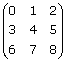
Matriser med bara en rad kallas radmatris eller alternativt radvektor som t ex
och matrisen med bara en kolonn som t ex
kallas kolonnmatris alternativt kolonnvektor.
Med rangen av en matris menas antalet linjärt oberoende rader (eller ekvivalent kolonner). För en n×n-matris kan man definiera determinanten som är icke-noll om och endast om rangen är maximal (n).
MATRISOPERATIONER
Addition
Två matriser A, B vilkas rad- resp. kolonnantal är lika kan alltid adderas:
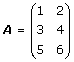
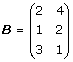
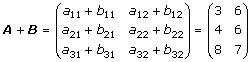
Eftersom additionen sker elementvis så kommer varje räkneregel som gäller för addition av reella (komplexa) tal även att gälla för matriser. Speciellt så gäller kommutativa lagen A + B = B + A och associativa lagen (A + B) + C = A + (B + C).
Matriser där alla element är 0 kallas för nollmatrisen och betecknas med 0 oavsett storlek:
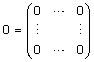
A - A = 0
Multiplikation
Multiplikation mellan matris och skalär utförs så att man multiplicerar alla element i matrisen med skalären.
Produkten AB kan bildas endast om antalet kolonner i A överensstämmer med antalet rader i B. Om A och B är kvadratiska matriser av samma typ kan man bilda både AB och BA (i allmänhet olika).
Matrismultiplikationen AB = C där elementet cik i C beräknas genom att
Exempel:
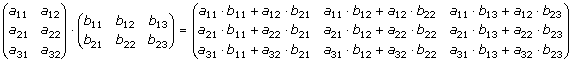
AB ≠ BA,
däremot associativ och distributiv (om A, B och C är kvadratiska matriser av samma typ (ordning):(AB)C = A(BC),
(A + B)C = AC + BC och A(B + C) = AB + AC
Ett ekvationssystem kan uttryckas i matrisform:
Exempel:
som med matriserna:
Ax = b
Matrispotens
n:e potensen av en matris menas produkten av n kvadratiska matriser:An = AA…A
Enhetsmatris
Enhetsmatrisen, E är en kvadratisk matris med ettor på huvuddiagonalen (från övre vänstra till nedre högra hörnet) och nollor på alla andra övriga platser i matrisen, med annat ord Eik = δik (där δik är Kroneckers delta symbol).
Kroneckers delta-symbol ![]() där i och k är heltal.
där i och k är heltal.
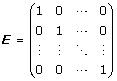
Man har att AE = EA = A för alla matriser A som kan multipliceras med E.
Beteckningen I för enhetsmatris förekommer också.
Inversmatris
A-1, inversen av den kvadratiska matrisen A, definieras av att A A-1 = A-1A = E (E är den enhetsmatris). Finns det en matris A-1 som uppfyller ekvationerna så sägs A vara inverterbar.
En kvadratisk matris kallas reguljär eller icke-singulär om inversmatris
existerar.
En matris A är inverterbar om och endast om
determinanten för matrisen är ej noll.
det A ≠ 0
Med hjälp av en invers erhåller man lösningen till ekvationssystemet Ax = b ovan som x = A-1b.
Adjunkt matrisAdjungerade matrisen till
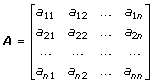
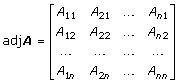
![]() och
och ![]()
Exempel: Räkna ut inversen av matris 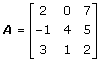
Lösning: Matrisen är reguljär, det A = -85 ≠ 0.
Elementerna av adjungerade matrisen är:
Inversmatrisen är: 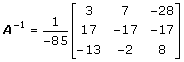
Transponering
Om vi i matrisen A av typ m×n låter rader och kolonner byta plats får vi en n×m-matris som kallas de till A transponerade matrisen (A-transponat) och betecknas AT.
En kolonnvektors transponat är en radvektor.
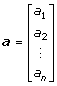
![]()
En matris är symmetrisk om A = AT
Om en kvadratisk matris A är sådan att alla element utanför diagonalen är noll, alltså om aij = 0 för i ≠ j, kallas A en diagonalmatris.
t ex
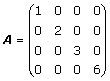
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |