| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| Ellips Parabel Hyperbel |
Kägelsnitt - andragradskurvor |
Kägelsnitt
Ett kägelsnitt (eller en andragradskurva) är skärningen mellan ett plan och en cirkulär konisk yta.
De tre huvudtyperna av kägelsnitt - ellips (och cirkel), parabel och hyperbel - erhålls som skärningar mellan den koniska ytan och plan, som ej går genom den koniska ytans spets. Vilken typ av kägelsnitt som erhålls beror på den skärande planets lutning.
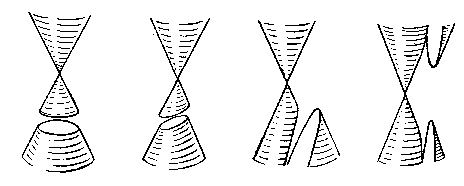
Kägelsnitten kan också definieras geometriskt i planet. Man har givet en punkt i planet (fokus [focus pl. foci] eller brännpunkt) och en rät linje (direktris eller styrlinje) och söker orten för de punkter, som är sådana som, att deras avstånd till brännpunkten och styrlinjen står i konstant förhållande e.
e är kägelsnittets excentricitet.
Cirkeln betraktas som en ellips med excentriciteten 0, dess styrlinje kan anses ligga i oändligheten.
| ellips | parabel | hyperbel |
 |
 |
 |
| e = |
e = |
e = |
Andragradskurva
Andragradskurva, (med andra ord:kägelsnitt) är en plan kurva som i analytisk geometri beskrivs av en ekvation av typen
ax² + bxy + cy² + dx + ey + f = 0.
Diskriminanten (D = b² - 4ac) visar att kurvan kan vara
ellips (eller cirkel) om D < 0,
parabel om D = 0 och
hyperbel om D > 0.
Ellips
Ellipsen är ett kägelsnitt med excentriciteten e mellan 0 och 1.
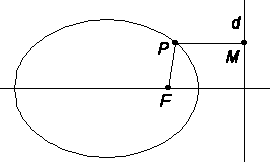
Ellipsens definitionEn ellips är orten för punkter i planet, vilkas avstånd till två givna punkter har en konstant summa.
F'P + PF = V'V = konstant
De fasta punkterna kallas brännpunkter (fokus) och de räta linjer, som från en punkt på ellipsen dragas till brännpunkterna kallas brännpunktsradier.
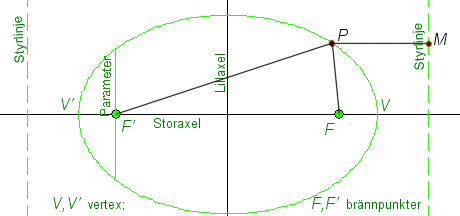 |
Ellipsen är symmetrisk kring linjen genom brännpunkten vinkelrät mot styrlinjen; denna linje skär ellipsen i två punkter V och V', var och en kallad vertex. Sträckan från V till V' kallas storaxel (större axel). Mittpunkten på storaxeln kallas ellipsens medelpunkt eller centrum. En korda är en sträcka som förenar två punkter på ellipsen. Kordan genom medelpunkten (syn. för centrum) vinkelrät mot storaxeln kallas lillaxeln (mindre axel). |
Med ellipsens excentricitet e förstås förhållandet mellan avståndet mellan brännpunkterna och storaxeln (e = c/a).
Med parametern till en ellips kallas den brännpuntskorda (fokalkorda), som är vinkelrät mot storaxeln.
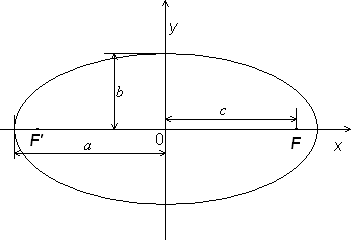 |
Ellipsens ekvation I den analytiska geometrin låter man i regel ellipsen vara så placerad i koordinatsystemet att medelpunkten sammanfaller med origo och storaxeln med x-axeln. Dess ekvation blir då där 2a är längden av storaxeln och 2b ländgen av lillaaxeln, och a är större än b. Avståndet c från medelpunkten till ena brännpunkten och excentriciteten e ges då av ekvationerna |
Avståndet från medelpunkten till styrlinjen är ![]() och parameterns längd är
och parameterns längd är ![]()
Parabel
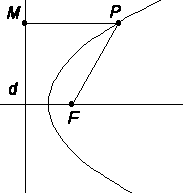
Parabeln är ett kägelsnitt med excentriciteten 1.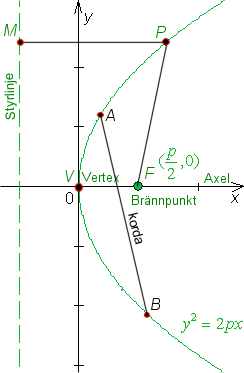 |
En parabel är orten för de punkter, som ligger lika långt från en given punkt och från en given rät linje i planet. Den givna punkten kallas brännpunkt eller fokus och den givna linjen styrlinje eller direktris. Parabelns form beror endast av det avståndet (p) från brännpunkten till styrlinjen. Ekvationen för en tangent till en parabel är yy1 = p(x + x1), om x1 och y1 är tangeringspunktens koordinater. |
Översikt över parabelekvationer:
| Ekvation | Symmetri- axel |
Fokus | Öppning | Styrlinje | 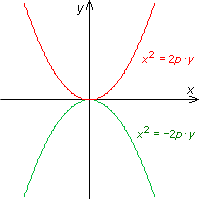 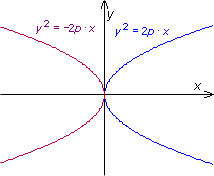 |
|
| x² = 2p·y | y-axeln | (0, p/2) | Uppåt | y = - p/2 | ||
| x² = - 2p·y | y-axeln | (0, -p/2) | Nedåt | y = p/2 | ||
| y² = 2p·x | x-axeln | (p/2, 0) | Åt höger | x = - p/2 | ||
| y² = - 2p·x | x-axeln | (- p/2, 0) | Åt vänster | x = p/2 | ||
| (x - a)² = 2p(y - b) | (a, b + p/2) | Uppåt | y = b - p/2 | |||
| (x - a)² = - 2p(y - b) | (a, b - p/2) | Nedåt | y = b + p/2 | |||
| (y - b)² = 2p(x - a) | (a + p/2, b) | Åt höger | x = a - p/2 | |||
| (y - b)² = - 2p(x - a) | (a - p/2, b) | Åt vänster | x = a + p/2 |
Koordinaterna för parabelns vertex fås genom skärningspunkten mellan parabeln och symmetriaxeln.
Andragradsekvation i allmän form:
y = ax² + bx + c
beskriver en parabel som har parameter: ![]() koordinater av vertex:
koordinater av vertex: ![]()
Hyperbel
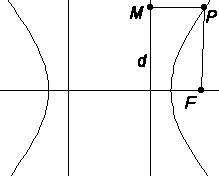
Hyperbeln är ett kägelsnitt med excentriciteten e större än 1.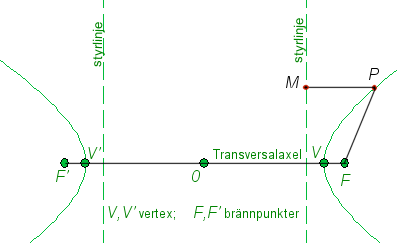 |
Orten för en punkt P, vars avstånd från två fasta punkter F, F' (fokus eller brännpunkter) har en konstant skillnad, kallas hyperbel. |FP - PF'| = VV' Hyperbeln är symmetrisk kring linjen genom brännpunkten. Denna linje skär hyperbeln i två punkter, vertex. Sträckan som förenar de båda vertex kallas transversalaxel. Mittpunkten på transversalaxeln kallas centrum eller medelpunkt. En korda är en sträcka som förenar två punkter på hyperbeln. |
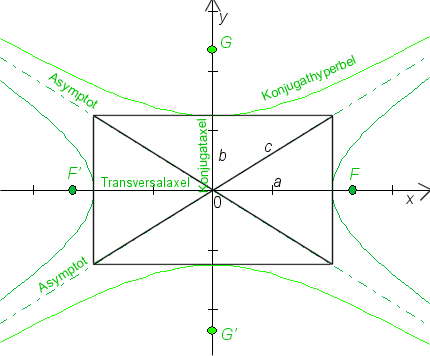
| Hyperbelns ekvation I den analytiska geometrin låter man i regel hyperbeln vara så placerad att medelpunkten sammanfaller med origo och transversalaxeln med x-axeln. Hyperbelns ekvation blir då där 2a är längden av transversalaxeln och 2b längden av konjugataxeln, en sträcka vinkelrät mot transversalaxeln och delad mitt itu av medelpunkten. Avståndet c från medelpunkten till ena brännpunkten och excentriciteten e kan uttryckas i storheterna a och b genom ekvationerna Den konstanta skillnaden |PF-PF'| = 2a. |
 |
De parametriska ekvationer för en hyperbel:
| x = a·cosh t | y = b·sinh t |
| eller | |
| x = a·sec t | y = b tan·t |
En hyperbel har två asymptoter. Dessa är de räta linjerna genom origo med ekvationerna ![]() respektive
respektive ![]() .
.
Asymptot är ett rät linje, som kurvan närmar sig mot oändligheten, så att kurvans avvikelse från linjen kan göras hur liten som helst, blott man följer kurvan tillräckligt långt bort.
Till varje hyperbel hör en konjugathyperbel, som har hyperbels konjugataxel som transversalaxel och dess transversalaxel som konjugataxel. Dess ekvation är| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |