WolframAlpha Lexikon Formler Terminologi länkar Svenska matematiklänkar Math. Resources on the Internet Böcker

Gästbok
Matematik minimum - Terminologi
En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik
A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö     
Klicka på någon av bokstäverna
 Nedladdning

Talet e (nepers tal, Eulers tal)
 Logaritm

Talet e, i matematiken är beteckningen för basen för de naturliga logaritmerna, med decimalbråksutvecklingen 2,718 281 828 459…

Det finns många analytiska uttryck för e, t.ex. serieutvecklingen

De flesta kvantiteter i naturen ökas eller minskas på sådant sätt att förändringens hastighet minskas (eller ökas) i tiden beroende av sin storhet. Till exempel ett uppvärmt föremål kylar sig hälften av sin temperatur under en viss tid och det behöver lika lång tid att kyla ner ytterligare hälften dess temperatur. Värmeöverföring är proportionell mot temperaturskillnad. De flesta förändringar i naturen är likadana, de är proportionella mot förändrande storheterna.

Vi kan anta att det finns en idealiskt isolerad vattenbehållare som innehåller 100 liter 100 ºC vatten. Om genom en kran tömmer vi ut en tiondel av innehållet, 10 liter 100 ºC vattnet och genom en annan fyller vi 10 liter 0 ºC vatten får vi 100 liter 90 ºC vatten. Upprepar vi det, tömmer vi ut 10 liter 90 ºC och ersätter det vi med 0 ºC vatten då skall ha behållaren 100 liter 81 ºC vatten eftersom 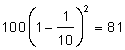. Om vi släpper ut tio gånger en tiondel av innehållet och ersätter det varma vattnet med kallt (0 ºC) blir vattnets temperatur 34,87 ºC eftersom 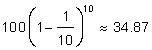. Om vi släpper ut bara en tjugondel av vattnet ett tag och ersätter vi tjugo gånger med kallt vattnet blir till slut en lite varmare 35,85 ºC efter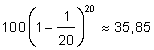som . Vid kontinuerlig uttömning av varmt vatten efter 10 minuter med t.ex. 10 liter/minut vattenflöde och ersättning med kallt vatten kan räknas ut till 36,79 ºC eftersom 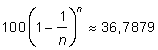om n är oändligt stort.

Med införande av talet e (e ≈ 2,718281828…) med definition
  eller     (se gränsvärde för limes)

blir lätt att räkna ut alla liknande uppgifter, eftersom den exponentiella funktionen beskriver de alla förändringar som är proportionella mot värden av en storhet (t.ex. temperatur, hastighet, elektrisk laddning, folkmängd) och minskas eller ökas i tiden, då konstanten A är storhetens och B är riktningskoefficintens begynnelsevärde.

Med formel kan vi beskriva ovanstående och alla liknande temperatursminskning:
där ϑ0 är begynnelse temperaturskillnad, ϑ är temperaturskillnad, t är tiden och T är en karakteristisk tid under vilken temperaturen sjunker 36,8 %.
         

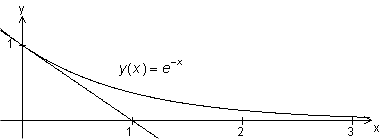
Exemplar:

Då kan vi räkna ut även att vilken tidpunkt kommer 25 ºC vatten ur kranen: (se exemplet ovan)

Eller om ett föremåls hastighet bromsas ner under 3 sec från v0 = 80 km/h till v = 10 km/h från formel kan den karakteristiska tiden ("tidkonstanten") räknas ut för bromsning T = 1,44 sec och att under 2 sec vid samma bromsning minskar hastigheten till 20 km/h.

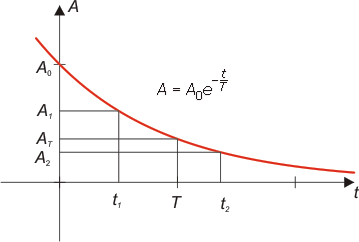
Givna A1, A2, t1, t2 (A1 > A2, t1 < t2)
Sökta T och A0 (karakteristisk tid och begynnelsevärde)

 

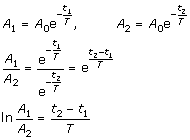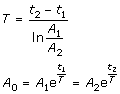av Bruno Kevius
All kopiering tillåten!   
 Matematiklexikon:
A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö
Klicka på någon av bokstäverna		    Svenska Matematiklänkar