WolframAlpha Lexikon Formler Terminologi länkar Svenska matematiklänkar Math. Resources on the Internet Böcker

Gästbok
Matematik minimum - Terminologi
En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik
A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö     
Klicka på någon av bokstäverna
 Nedladdning

Periodiska funktioner - trigonometriska funktioner
- tidsperiodiska storheter

En funktion ƒ är periodisk med perioden p, om ƒ(x+p) = ƒ(x) för alla x  mängden av reella tal.

En periodisk funktion får samma värde, om en viss storhet, perioden eller en multipel av perioden adderas till eller subtraheras från den oberoende variabeln. Alltså det finns ett p så att ƒ(x+kp)=ƒ(x) för alla värden på variabeln x.
Funktionens period är p.

Grafen till ƒ är än periodisk kurva.

Amplituden är det största av absolutbeloppen |f(x)|;

frekvensen är 1/p, den inverterade talet till perioden.

 

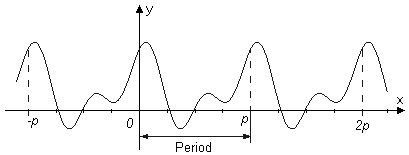Den enklaste periodiska funktionerna är de trigonometriska funktionerna, sinus- och cosinusfunktionerna. (Se Sinusformigt varierande tidsperiodiska storheter)
Sålunda är funktionen x -> cos x periodisk med perioden 2π (eller 360º); dess amplitud är 1 och dess frekvens 1/2π.
Funktionen x -> 3 sin 4πx är periodisk med perioden 1/2, amplituden 3 och frekvensen 2.
Allmännare är funktionerna x -> A sin (2πx/k) och x -> A cos (2πx/k) periodiska med perioden k och amplituden A; dessa funktioner är de s.k. enkla harmoniska funktionerna (harmoniska svängningarna).

Harmonisk funktion

En reell funktion av två variabler (x,y)->z(x,y), som satisfierar Laplaces ekvation

I allmänhet förutsätts också, att z har kontinuerliga partiella derivator av första och andra ordningen i något område av xy-planet.
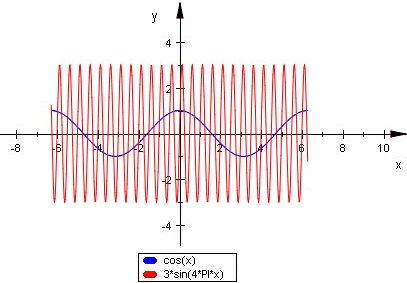För alla k reella tal i funktionerna: z = ekxcos(ky) och z = ekxsin(ky)

Ex för z = ekxcos(ky)

 

 

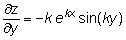
av Bruno Kevius
All kopiering tillåten!   
 Matematiklexikon:
A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö
Klicka på någon av bokstäverna		    Svenska Matematiklänkar