WolframAlpha| WolframAlpha |
Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
 Gästbok |
Nedladdning
|
|
Tidsperiodiska storheter Periodiska växelstorheter |
- periodiska funktioner - storheter |
Benämningar och beteckningar av värdena av allmänna tidsperiodiska storheter
| momentanvärde (ögonblicksvärde) | a | (värdet av en i tiden variabel storhet vid en given tidpunkt) |
| toppvärde (maximivärde, amplitud) | â | (toppvärde och bottenvärde är de högsta och lägsta värdena, amplitud är den maximala avvikelsen från medelvärdet) |
| bottenvärde (minimivärde) | ǎ | Betecknas även med index min (amin). |
| effektivvärde | A, ã | Betecknas även utan ~ med index eff (Aeff, ARMS). |
| aritmetisk medelvärde | ā | Beteckning utan ¯ och med index av rekommenderas ej. |
| medelbelopp | |ā| | Benämningen likriktad medelvärde rekommenderas ej. |
| ^ | tak |
 |
bock |
| ~ | våg, ("tilde" efter spansk bruk) |
Sinusformigt varierande tidsperiodiska storheter
En godtycklig fysikalisk storhet a (ström, spänning, flöde etc.) som varierar sinusformigt med tiden (sinusformad växelstorhet), används samma beteckningsätt som för allmänna tidsperiodiska storheter.
(eller med cosinusfunktionen som ofta lämpar sig bättre)
|
 |
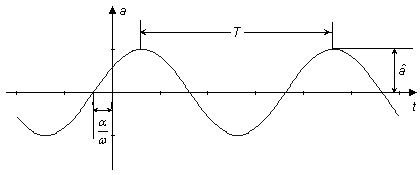Tiden för en period, perioden eller periodtiden
Antalat perioder per sekund, periodtalet eller frekvensen
Enheten för frekvensen är 1 hertz (1 Hz)
En växelstorhets effektivvärde är dess kvadratiska medelvärde
(Effektivvärdet av en växelstorhet är lika med värdet av en oföränderlig storhet som utvecklar lika effekt under samma period, i samma förhållande.)
En växelstorhets medelbelopp (beloppsmedelvärde, likriktade medelvärde) är dess aritmetiska medelvärde, bestämt sedan man ändrat tecken på storhetens alla negativa delar.
För en växelstorhet med två lika halvperioder är medelbelopp:
|
 |
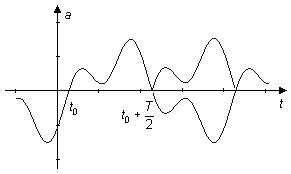Grafisk behandling av sinusformigt varierande storheter med visardiagram
En sinus formad växelstorhet a = A represanteras grafiskt genom en visare dvs en i planet belägen riktat sträcka med längden A, som bildar vinkeln α med den horisontella axeln. (Visaren roterar relativt projektionslinjen med vinkelhastigheten ω. Om endast vinkeln ωt + α är av intresse, kan endera av dessa vara stillastående. Ofta intresserar ej momentanvärdet utan endast effektivvärdet och fasvinkeln, och man rättar då visarens längd efter effektivvärdet.) |
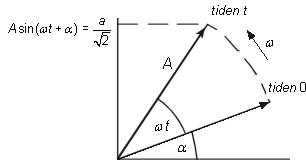 Om fasvinkeln α = 0, är växelstorheten riktfas. Tillhörande visare ligger längs horisontella axeln. |
Redan en enda visare och dess projektionslinje bildar ett visardiagram. Ett sådant innehåller dock oftast flera visare för samhörande storheter av samma frekvens. Projektionslinjen är då gemensam och kan utelämnas, om endast de inbördes relationerna är av intresse. I vissa fall, t ex vid modulering, kan visare representerande storheter av olika frekvens förekomma.
Matematiska operationer med sinusformiga storheter svarar mot geometriska operationer, visaroperarioner, med motsvarande visare.
|
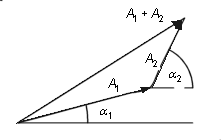
Addition av två eller flera momentanvärden motsvarar sammansättning enligt parallellogramlagen, "vektoriell addition", av de visare vilkas projektioner representerar momentanvärdena (Begreppen visare och vektorer får inte för den skull sammanblandas.) Vid addition eller substraktion av två sinusformade storheter med samma vinkelfrekvens ω 
Dess visare A1 + A2 (resp A1 - A2) erhålls genom geometrisk addition resp. geometrisk substraktion av visarna A1 och A2. |
  |
rad) framåt resp bakåt i rotationsriktningen relativt projektionslinjen. En sådan överföring kan
uppfattas som användning av en tänkt operator, en visaroperator, som definieras av den verkan den åstadkommer
och som kan grafiskt representeras av en visare.
|
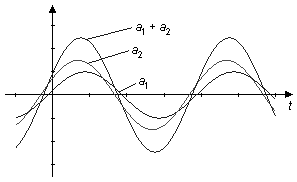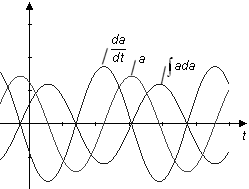
Vid derivation med avseende på tiden av en sinusformad storhet
a = A
uppkommer en ny sinusformad storhet med samma vinkelfrekvens
 sin (ωt + α) = ωAsin (ωt + α + )Vid integration med avseende på tiden av en sinusformad storhet a uppkommer en ny sinusformad storhet med samma vinkelfrekvens  =  sin (ωt + α - ) |
 |
Analitisk behandling av sinusformade växelstorheter med komplexa tal
Momentanvärdet a = a cos(ωt + α) av en sinusformigt varierande storhet kan uppfattas som den reella delen av ett komplext momentanvärde a = â exp i (ωt + α).
En sinusformad växelstorhetsin (ωt + α)
α
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |
