| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| Principalvärdena Räknerlagar för cyklometriska funktioner Expansion i potensserier Komplexa variabler |
Cyklometriska funktioner (Arcusfunktioner) |
Trigonometriska funktioner Hyperboliska funktioner |
Inversa trigonometriska funktioner
| Om en trigonometrisk funktion "vänds", på samma sätt som man kan uttrycka y = ln x som x = ey eller y = x² som x = En vinkels storlek kan anges i bågmått, där vinkeln sättes lika med motsvarande båglängd i enhetscirkeln. De inversa funktionerna till de trigonometriska funktionerna kallas cyklometriska funktioner eller arcusfunktioner: |
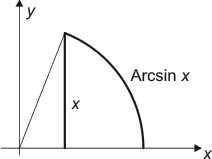 |
Arcus sinus (Arcsin, ArcSin, arcsin, asin, sin-1) för x
är en vinkel (en båglängd) vars sinus är x.
T.ex. arcsin ½ är lika med 30º, 150º, eller i allmänt n180° + (-1)n30°.
Arcus cosinus (Arccos, ArcCos, arccos, acos, cos-1) för x
är en vinkel (en båglängd) vars cosinus är x.
T.ex. arccos ½ är lika med 60º, 300º, eller i allmänt n360° ± 60°.
Arcus tangens (Arctan, ArcTan, arctan, atan, arctg, tan-1) för x
är en vinkel (en båglängd) vars tangens är x.
T.ex. arctan 1 är lika med 45º, 225º, eller i allmänt n180° + 45°.
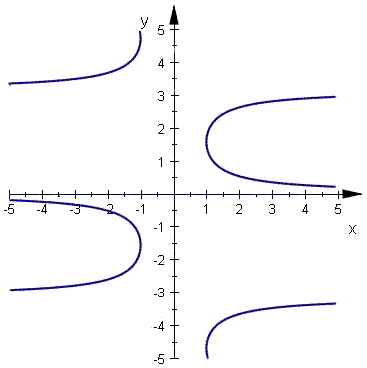
Arcus cotangens (Arccot, ArcCot, arccot, arcctg, actg, arccotg, ctg-1, cot-1) för x
är en vinkel (en båglängd) vars cotangens är x.
T.ex. arccot 1 är lika med 45º, 225º, eller i allmänt n180° + 45°.
Arcus secans (Arcsec, ArcSec, arcsec, asec, sec-1) för x
är en vinkel (en båglängd) vars secans är x.
T.ex. arcsec 2 är lika med 60º, 300º, eller i allmänt n360° ± 60°.
Arcus cosecans (Arccsc, ArcCsc, arccsc, arccosec, acsc, csc-1) för x
är en vinkel (en båglängd) vars cosecans är x.
T.ex. arccsc 2 är lika med 30º, 150º, eller i allmänt n180° + (-1)n30°.
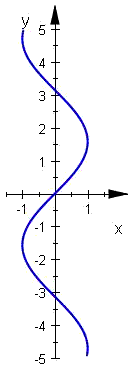 |
 |
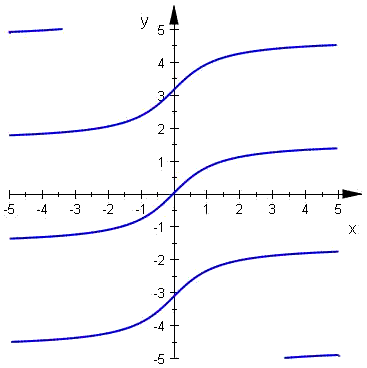 |
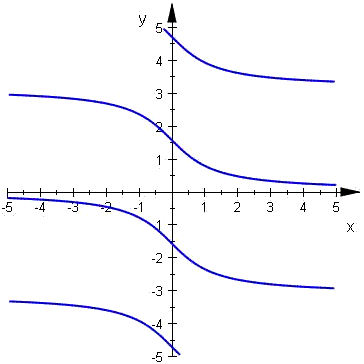 |
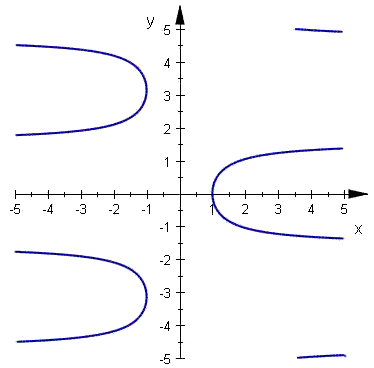 |
 |
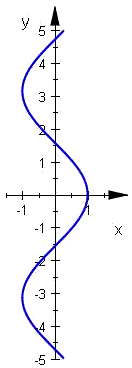
| Arcus sinus | Arcus cosinus | Arcus tangens | Arcus cotangens | Arcus secans | Arcus cosecans |
Principalvärdena av inversa trigonometriska funktioner
Eftersom de trigonometriska funktionerna är periodiska, blir arcusfunktionerna oändligt mångtydiga (flertydiga). För att undvika detta utväljer män s.k. principalvärdena, som begränsas till principalvärdena betecknas ofta med små begynnelsebokstäver medan de inversa funktioner beteckans ofta med stora begynnelsebokstäver, och definieras på så sätt:
| Definitionsområde | Värdeförråd (värdemängd) | ||
| arcsin x | arcus sinus för x | -1 ≤ x ≤ 1 | y = arcsin x  x = sin y, -π/2 ≤ y ≤ π/2 x = sin y, -π/2 ≤ y ≤ π/2Funktionen arcsin är den inversa funktionen till sin men den ovan nämnda begränsningen. |
| arccos x | arcus cosinus för x | -1 ≤ x ≤ 1 | y = arccos x  x = cos y, 0 ≤ y ≤ π
x = cos y, 0 ≤ y ≤ πFunktionen arccos är den inversa funktionen till cos men den ovan nämnda begränsningen. |
| arctan x | arcus tangens för x | -∞ < x < ∞ | y = arctan x  x = tan y, -π/2 < y < π/2 x = tan y, -π/2 < y < π/2Funktionen arctan är den inversa funktionen till tan med den ovan nämnda begränsningen. |
| arccot x | arcus cotangens för x | -∞ < x < ∞ | y = arccot x  x = cot y, 0 < y < π x = cot y, 0 < y < πFunktionen arccot är den inversa funktionen till cot med den ovan nämnda begränsningan. |
| arcsec x | arcus secans för x | x ≤ -1 eller x ≥ 1 | y = arcsec x  x = sec y, 0 ≤ y ≤ π x = sec y, 0 ≤ y ≤ πFunktionen arcsec är den inversa funktionen till sec med den ovan nämnda begränsningan. |
| arccosec x | arcus cosecans för x | x ≤ -1 eller x ≥ 1 | y = arccsc x  x = csc y, -π/2 ≤ y ≤ π/2 x = csc y, -π/2 ≤ y ≤ π/2Funktionen arcsec är den inversa funktionen till sec med den ovan nämnda begränsningan. |
På så sätt definieras arcsin x som principalvärdet av Arcsin x genom att det krävs att dess värden skall ligga mellan -π/2 och π/2. Definitionsområdet är intervallet [-1, 1] och arcsin x är en växande funktion där med derivatan ![]() .
.
Exempel: ![]() ty
ty ![]() och 0 <
och 0 < ![]() < π
< π
Samband mellan inversa trigonometriska funktioner och deras principalvärde är:
| Arcsin x | = | (-1)narcsin x + πn |
| Arccos x | = | ±arccos x + 2πn |
| Arctan x | = | arctan x + πn |
| Arccot x | = | arccot x + πn |
| Arcsec x | = | ±arcsec x + 2πn |
| Arccsc x | = | (-1)narccsc x + πn |
Relationer mellan principalvärdena av inversa tirgonometriska funktioner
arcsin x = - arcsin (-x) = ![]() - arccos x = [arccos √1 - x²]* = arctan
- arccos x = [arccos √1 - x²]* = arctan ![]() = [arcctg
= [arcctg ![]() ]*
]*
arccos x = π - arccos (-x) = ![]() - arcsin x = [arcsin √1 - x²]* = [arctan
- arcsin x = [arcsin √1 - x²]* = [arctan![]() ] = arccot
] = arccot ![]()
arctan x = -arctan (-x) = ![]() - arccot x = arcsin
- arccot x = arcsin ![]() = [arccos
= [arccos ![]() ]* = [arcctg
]* = [arcctg ![]() ]*
]*
[ ]* gäller endast om x är positiv
Expansion i potensserier
Principialvärdena kan expanderas i potensserier:
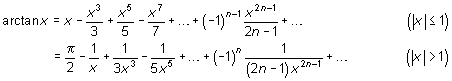
Komplexa variabler
Definitionerna av de inversa trigonometriska funktionerna av komplexa variabler är samma som definitionerna av funktionerna av de reella variabler.
Till exempel w = Arc sin z, om z = sin w.
Dessa funktioner har oändliga värde och kan uttryckas på följande sätt i logaritmerna:
| Arc sin z = - i Ln (iz + √1 - z²), | arc sin z = - i ln (iz + √1 - z²), | |
| Arc cos z = - i Ln (z + √z² - 1), | arc cos z = - i ln (z + √z² - 1), | |
| Arc tan z = |
arc tan z = |
|
| Arc cot z = |
arc cot z = |
Exemplar:
arc sin (3) ≈ 1,570796327 - 1,762747174 i,
arc cos (1 + i) ≈ 0,9045568943 - 1,061275062 i,
arc sin (i) = ln(1+√2) i;
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |