| Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
Gästbok |
Nedladdning |
|
| areafunktionerna kedjelinjen |
Hyperboliska
och inversa hyperboliska funktioner
|
Trigonometriska funktioner Hyperbel |
Hyperboliska funktioner definierade med hjälp av enhetshyperbeln (x² - y² = 1)
| Liksom trigonometrisk sinus och cosinus kunna betraktas som koordinater för en utefter enhetscirkeln löpande punkt, kunna hyperbolisk sinus och cosinus uppfattas som koordinater för en utefter den liksidiga hyperbeln (enhetshyperbeln = x² - y² = 1) löpande punkt. | 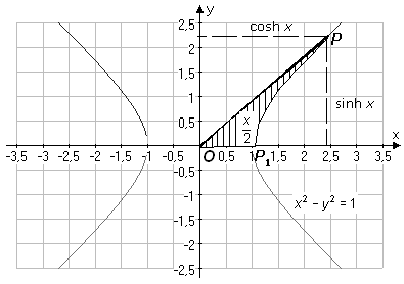 |
Definition:
|
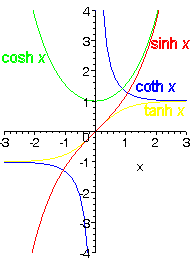 |
Serier:De hyperboliska funktionerna har inga reella perioder. Däremot har sinh x och cosh x perioden 2π i och tanh x och coth x perioden π i. (i är den imaginära enheten)
; gäller för alla x
; gäller för alla x
Hyperbelsektorns area
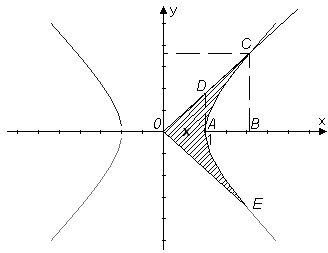 |
Arean x (streckat på figuren) kan räknas ut med hjälp av integraler*: därifrån _______________________ * |
Formler
De inversa hyperboliska funktionerna (areafunktionerna)
De kallas så på grund av sitt sammanhang med hyperbelsektorns area
Definitioner och benämningar
| alternativa beteckningar: | ||||
| Räknedosor | Maple Mathematica MuPad |
MathCad Matlab |
||
| y = arsinh x = |
area sinus hyperbolicus, betyder, att x = sinh y |
sinh-1 x | arcsinh x | asinh x |
| y = arcosh x = |
area cosinus hyperbolicus, betyder, att x = cosh y |
cosh-1 x | arccosh x | acosh x |
| y = artanh x = |
area tangens hyperbolicus, betyder, att x = tanh y |
tanh-1 x | arctanh x | atanh x |
| y = arcoth x = |
area cotangens hyperbolicus, betyder, att x = coth y |
coth-1 x | arccoth x | acoth x |
| y = arsech x | area secans hyperbolicus, betyder, att x = sech y |
sech-1 x | arcsech x | asech x |
| y = arcosech x | area cosecans hyperbolicus, betyder, att x = cosech y |
csch-1 x | arccsch x | acsch x |
Kedjelinjen
| är en plan kurva, som intas av en kedja, som under linverkan av enbart tyngdkrafter hänger mellan två punkter. Ekvationer för en kedjelinje kan uttryckas med hjälp av den s k hyperboliska cosinusfunktionen: |
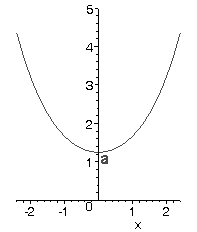 |
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |