WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

Integral till en given storhet kallas en annan storhet, vars derivata är lika med den givna. Så är t. ex. x² integralen till 2x, eftersom 2x är derivatan av x².

Derivatan (ƒ’) av en funktion ƒ anger hur funktionens värde (ƒ(x)) varierar när värdet på x förändras.
Integralen är egentligen är kontinuerliga summor av förändringarna, förutsatt att förändringar är beräknbara från förändringens mått (derivatan). ∫ƒ’(x)dx = ƒ(x)

Exemplar för kontinuerliga summor

Längden AB är summan av dellängder:

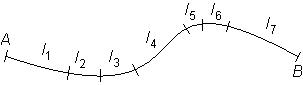
med summan av n stycken obestämda Δl längder är 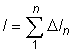och när längden av Δl går mot 0 (dl, och n går mot ∞) då summan "går mot" integralen 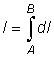kallas integraltecken.

Båglängden av explicit given [y = ƒ(x) eller x = g(y)] eller i parameterform [x = φ(t), y = ψ(t)] kurva:

eller L = ∫ dl där dl² = dx² + dy²

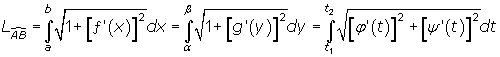
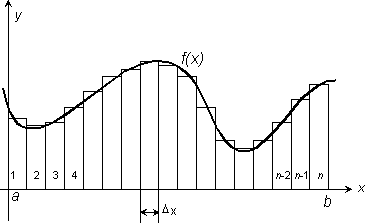Summan av arean av n stycken rektanglar vars höljd är f(xi) och bredd är Δx.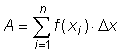 och när Δx går mot 0 då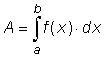

Integral av trappfunktioner

En funktion Φ på intervallet [a, b] kallas en trappfunktion (ibland sträckvis konstant funktion) om det finns en indelning av [a, b] i mindre delintervall på vilket Φ har ett konstant värde. Mer precist, om delningspunkterna är

a = x₀ < x₁ < … < x_n-1 < x_n = b,

definieras Φ av

Φ(x)= c_k     då     x_k-1 < x < x_k      k = 1,…,n,

Talet

kallas integralen av trappfunktionen Φ.

Riemannintegralen

En begränsad funktion ƒ definierad på ett ändligt intervall [a, b] säges vara (Riemann)integrerbar över detta om det till varje reellt tal ε > 0 finns trappfunktioner Φ och Ψ som satisfierar

Φ(x) ≤ ƒ(x) ≤ Ψ(x),       a ≤ x ≤ b

och som är sådana att

I(Ψ) - I(Φ) < ε

Primitiv funktion

Funktionen F är en primitiv funktion till ƒ om derivatan av F är ƒ.
Den obestämda integralen till funktionen ƒ (med avseende på x) betecknas .

när

där funktionen ƒ(x) kallas för integrand. C kallas integrationskonstant och x kallas integrationsvariabel.

T.ex. är då

Om F(x) är en primitiv funktion till f(x), gäller att
F(x) + C
också är en primitiv funktion till ƒ(x) för alla reella konstanter C.

Obs! F kallas en primitiv funktion men inte den primitiva funktionen.
Vi skriver som beteckning för samtliga primitiva funktioner till ƒ(x).

Integrationsregler för primitiva funktioner

1. En konstant faktor får flyttas ut framför integraltecknet:

2. Integralen av en summa är lika med summan av integralerna:

3. Variabelsubstitution:   (Variabeln ersätts med en funktion)
    om x = φ(t) då

4. Partiell integration (Partialintegration):

Partiell integration svarar mot produktregeln bland deriveringsreglerna: (ƒg)' = ƒ'g + ƒg' kan ju också skrivas: ƒg' = (ƒg)' - ƒ'g.

Standardintegraler

Potensfunktioner	Exponentialfunktioner
Trigonometriska funktioner	Hyperboliska funktioner
Rationella funktioner	Irrationella funktioner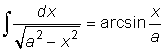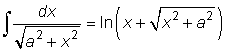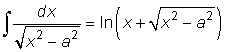

The Integrator
Lös integraler direkt på nätet!
http://integrals.wolfram.com/

Integrationsmetoder

1. Om det är känt att (t.ex. från tabel) då

Exemplar:

2. Om integrand är ett bråk vars täljare är derivata av nämnare då integral är lika med logaritmen av nämnaren

Exempel:

Bestämd integral

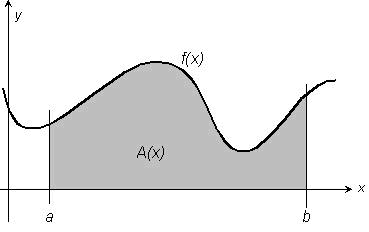
Den bestämda integralen av en funktion mellan två gränser är en storhet som kan tolkas som arean mellan funktionskurvan och x-axeln mellan samma gränser (arean under x-axeln räknas negativ).

Den bestämda integralen definieras principiellt som gränsvärdet av en summa. (Då de summerade elementens storlek går mot noll går deras antal mot oändligheten.) Med bestämda integraler beräknas båglängder, ytor och volymer. De har dessutom stor användning vid många tillämpningar, t ex inom mekaniken för beräkning av tyngdpunkter, tröghetsmoment m m.

Integralen skrivs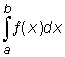 a och b kallas undre respektive övre integrationsgräns. Beräkning av en integral sker med hjälp av formeln 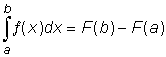varvid F är en primitiv funktion till funktionen ƒ i intervallet från a till b.