WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

Partiella derivator

Om en funktion av två eller flera variabler deriveras med avseende på en enda variabel, medan de andra betraktas som konstanta, erhålles en partiell derivata.
Den partiella differentialen betecknas med ∂, och ∂x utläses som "variationen av x", och partiella derivatan till en funktion av flera variabler u = ƒ(x,y,z, …,t) med avseende på x betecknas något av följande sätt:

  där

Och funktionens totala differentalen menas man:

Exempel: För funktionen
z = x³ + y³ + 2xy
Den partiella derivatan av z med avseende på x, erhålles om vi deriverar z med avseende på x och betraktar den andra variabeln y som en konstant.
= 3x² + 2y
Den partiella andraderivatan och den partiella tredjederivatan blir

Den partiella derivatan av z med avseende på y erhålles, om vi deriverar z med avseende på y och betraktar den andra variabeln x som konstant.
= 3y² + 2x     och vidare och vidare

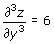
Om deriveras partiellt med avseende på y erhålles en derivata som brukar betecknas
Samma resultat erhålles om deriveras partiellt med avseende på x; vi har alltså
    Denna funktion brukar kallas den blandade andraderivatan.