WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

I matematiken beskriver en funktion sambandet mellan två eller flera variabler. Det är inte ett ömsesidigt samband utan den är en egenskap hos en variabel som är bestämd av en annan (eller av andra).

T.ex. resistansen (R) beror på temperaturen (T)
        hastigheten (v) beror på tiden (t)

Eftersom i matematiken är vanligt att en variabel inte har några andra egenskaper än att vara funktion, används vanligen samma bokstav för funktionsbeteckningen som för variabeln.

T.ex. det kvadratiska sambandet mellan variablerna x och y med olika funktionsbeteckning:

y = x²	y(x) = x²
y = ƒ(x)	ƒ(x) = x²
	y := x²
	F(x,y): x² - y = 0
y = ƒ	ƒ: x → x² (ƒ: x x²,  → )
	(,, {(x,x²,) : x })

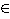
I skolmatematiken förekommer egendomliga definitioner av funktionen t.ex.:
"En relation, som ej innehåller två  par med samma första komponent men olika  andra komponent, är en funktion, (avbildning)."   (Matematikterminologi i skolan, 1966 SÖ)
"funktion - avbildning vars värden är tal."      (Matematiktermer för skolan, 2008 NCM).

Funktionsvärde (= beroende variabel)
Funktion av en variabel

En beskriven funktion är en regel, hur värdet av en variabel (beroende variabel eller funktionsvärde, {eng. dependent variable}, vanligen betecknas med y) bestäms med hjälp av värdet en annan variabel (oberoende variabel eller argument, {eng. independent variable}, vanligen betecknas med x).

I skolmatematiken visualiseras funktionen ofta som funktionmaskin med operator egenskap:
Oberoende variabel är en operand och kallas indata eller invärde och beroende variabel kallas utdata eller utvärde.

En storhet, y, som är på sådant sätt beroende av en annan, föränderlig storhet, x, att mot varje på ett givet sätt bestämt x-värde svarar ett (eller flera) bestämda värden på y, är en funktion av x.
Alltefter som mot varje värde på den oberoende variabeln svarar ett eller flera värden på funktionen, är denna entydig eller flertydig (mångtydig) (se Multivalued Function).

Enligt den moderna uppfattningen av funktionsbegreppet är:
En funktion (en avbildning) från en mängd X till en mängd Y är given, då man känner en otvetydig regel, som anger, hur varje element i X kan associeras (tillordnas) högst ett element i Y.
T.ex. Rotfunktionen F(x,y): x² + y² = 1, x → y kan betraktas som två skilda funktioner nämligen ƒ₁: x → √1 - x² och ƒ₂: x → - √1 - x²

Funktionsbeteckning

Vanligen betecknas funktionen med ƒ och funktionvärdet (beroendevariabeln) betecknas med ƒ(x).

Om funktionen betecknas med ƒ och oberoende variabeln betecknas med x, betecknas beroende variabeln med ƒ(x), alltså: y = ƒ(x), som utläses: "y är en funktion av x".

ƒ(x) utläses "f av x" eller kortare "f x"

ƒ(a) kallas funktionsvärdet för x = a.

Även andra beteckningar förekommer t. ex.: g, h, φ, ψ, F.
En del funktioner betecknas regelbundet med sina egna tecken, t. ex. de trigonometriska sinus (sin), cosinus (cos) o. s. v., t h e t a-funktionen (Θ), g a m m a-funktionen (Γ).

En storhet kan vara funktion av flera variabler, x, y, z, …, vilket då tecknas t. ex. V = ƒ(x,y,z, …).

Funktionsbeskrivning

• en tabell (värdetabell) eller
• en kurva i ett diagram (graf) eller
• med ett analytiskt uttryck (formel) av typen y = x² + 2 x - 3
     Är sambandet mellan x och y okänt kan det skrivas på formen y = ƒ(x) eller ƒ: x → y eller x → ƒ(x).

Exemplar:

Värdetabell: x oberoende variabel y beroende variabel -5 -4 -3 -2 -1 0 1 2 3 12 5 0 -3 -4 -3 0 5 12

Graf:

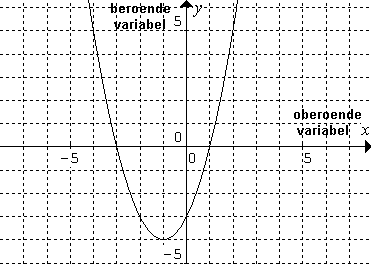Formel: y = x² + 2 x - 3   eller   ƒ: x  x² + 2 x - 3

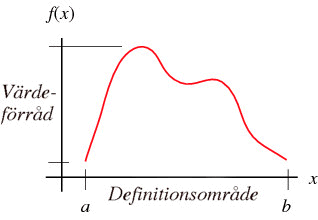
Definitionsområde eng. domain or range of the independent variable De tillåtna värdena av oberoende variabel (argument, x-värdena) kallas funktionens definitionsområde, definitionsmängd och betecknas med Df om funktionen betecknas med ƒ. T.ex.: 0 ≤ x eller x + eller Df = + Värdeförråd eng. range De erhållna värdena av beroende variabel (funktionsvärdena, y-värdena) kallas funktionens värdeförråd, värdemängd och betecknas med Vf om funktionen betecknas med ƒ. T.ex.: ƒ(a) < ƒ(x) < ƒ(b)     om     a < x < b       D = {x | a < x < b} Det kallas även målmängd i skolmatematiken.

Två funktioner ƒ och g är lika då och endast då D_f = D_g och ƒ(x) = g(x) för alla x D_f (= D_g)

Nollställe

Ett värde på den oberoende variabeln som ger funktionsvärdet noll, dvs. för funktionen ƒ en lösning till ekvationen ƒ(x) = 0.
Ibland används ordet rot i en liknande betydelse.

Explicit funktion
(explicit definierad funktion)

En reell funktion xy sägs vara explicit given, om den kan beskrivas av en ekvation, som är löst med avseende på y, dvs. av en ekvation på formen y = ƒ(x)

Exempel: Ekvationen y = 2x ger explicit en funktion xy.

Implicit funktion
(implicit definierad funktion)

När en beskrivande ekvationen för en funktion xy inte löst med avseende på y, sägs funktionen vara implicit given.

Exempel:

Ekvationen x² + y² - 1 = 0 definierar implicit en funktion xy.   Funktionen F(x, y): x² + y² = 1   (enhetscirkel). y kan inte lösas med avseende på x, varken eller kan beskriva hela funktionen.

explicit given funktion: y(x) = x² plotfunc2d(x^2, x = -3..3): 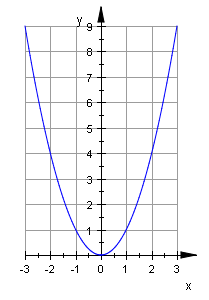MuPAD graphics

implicit given funktion: ƒ: (x,y) → x² + y² - 1 = 0 plot(plot::Implicit2d(x^2+y^2=1, x = -1..1, y = -1..1)); 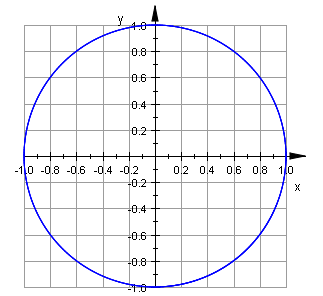MuPAD graphics

Parameterframställning
funktioner i parameterform

Vid framställningen av en plan kurva, ekvationer som ger koordinaterna för kurvans punkter som funktioner av en gemensam variabel, parameter.
Om man har x = φ(u) och y = ψ(u), så svarar mot varje u-värde en punkt i xy-planet, som bestämmes av funktionerna φ och ψ. När u varierar, beskriver denna punkt en kurva i xy-planet. Denna kurva presenterar en funktion y = ƒ(x). Man säger, att x = φ(u), y = ψ(u) är en parameterframställning av denna funktion.

Ex.:
x = sin  u
y = cos  u
    Genom elimination av u erhålls:
x² + y² = 1

Inversa funktioner

Om y är en funktion av x, kan också x betraktas som en funktion av y. Exempel: x = y³ : då är y = , vilket är den inversa funktionen till y = x³ Den inversa funktionen till ƒ betecknas ƒ-1. Denna beteckning bör ej användas om förväxling med 1/ƒ kan befaras. ƒ: x ex ƒ-1: x ln x g: x sin x        g -1: x arcsin x

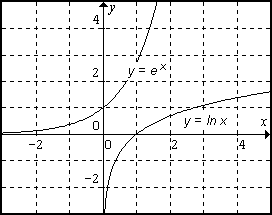Algebraiska funktioner

Algebraiska funktioner är
- polynomfunktioner (rationella hela funktioner),
- rationella funktioner (rationella bråk funktioner),
- rotfunktioner (algebraiska irrationella funktioner) t. ex. )
      och sammansättningar av dessa.

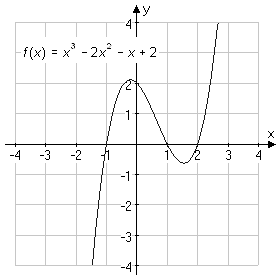
En polynomfunktion är en funktion, där funktionsuttrycket utgörs av ett polynom. En polynomfunktion kan alltid skrivas på den allmänna formen (normalformen): eller på den produktformen: Den högsta förekommande potensen av x anger polynomfunktionens grad. Restsatsen (Restteoremet)   Om en polynomfunktion p(x) divideras med (x - a) blir resten p(a). Bevis: där P(x) betecknar kvoten och R betecknar talresten. Genom multiplikation med (x - a) blir: p(x) = (x - a)·P(x) + R Detta är en identitet som alltså gäller även för x = a: p(a) = 0·P(x) + R = R
En linjär funktion är en polynomfunktion (av grad 1) av typen: ƒ(x) = ax + b (Den linjeära avbildningen från ett vektorrum till ett annat, kallas även för den linjära funktionen.)
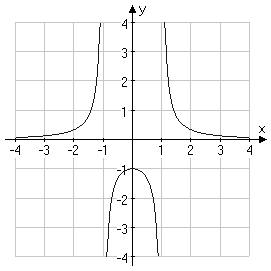
En rationell funktion är en funktion av typen: , där p(x) och q(x) är polynomfunktioner. En dylik funktion är definierad i alla punkter x, i vilka q(x) icke är lika med noll. Figuren visar grafen till den rationella funktionen , som är definierad överallt, utom punkterna 1 och -1.
Rotfunktioner, algebraiska irrationella funktioner Funktioner vars i förenklade explicit form rotutdragning förekommer, kallas irrationella funktioner. T. ex.  (a ≠ 0)
Grafen till funktionen avgörs av förtecknet av andragradstermens koefficienten (a) och diskriminanten. (D = b² - 4ac). hyperbel parabel hyperbel
Transcendenta funktioner De transcendenta funktionerna omfattar trigonometriska funktioner och exponentialfunktioner inklusive deras inversfunktioner. Dessa två funktionstyper utgörs i komplex analys av en funktionstyp eftersom eix = cos x + i sin x.
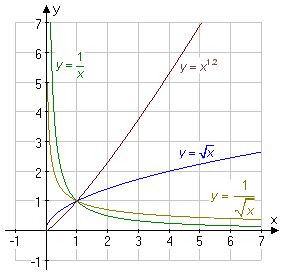
En potensfunktion är en funktion av typen: ƒ(x) = a·xb Om b är ett rationellt tal är funktionen algebraisk. På olika värden på b ändrar kurvorna karaktär:     b = -1 hyperbel b =  0 rät linje, parallell med x-axeln b = +1 rät linje genom origo med vinkelkoefficienten a b = +2 parabel med vertex i origo, symetrisk med avseende på y-axeln b = +3 kubisk parabel b = +½ parabelgren med vertex i origo Funktionerna ; ; y = x1.2; är exempel på potensfunktioner.

En exponentialfunktion är en funktion, där den oberoende variabel finns i exponenten. En exponentialfunktion kan skrivas som ƒ(x) = ax. Om basen a är negativ kan man definiera reella funktionsvärden endast för heltalsexponenter. Exponentialfunktionens allmänna form är      y = c e k x     eller     y = c a k x Exponentialfunktionen med basen e (nepers tal) betecknas även med exp x (ex = exp(x)). Logaritmfunktionen är inversen till exponentialfunktionen.     ƒ: x ax       ƒ-1: x logax, x>0.   Talet a är positivt och icke lika med 1; det kallas logaritmens bas. Vanliga baser är: - 10 (Briggs logaritmer, beteckning: lg x) - talet e (naturliga logaritmer, beteckning ln x) Den inversa funktionen till y = c e k x är logaritmfunktionen

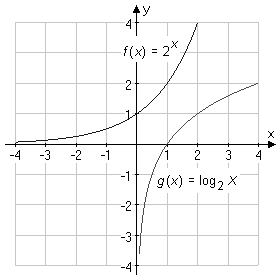Logaritmfunktionen satisfierar funktionalekvationen ƒ(A·B) = ƒ(A) + ƒ(B); den är den enda kontinuerliga funktionen, som satisfierar denna ekvation.

Sammansatta funktioner

Om en storhet y är en funktion av en annan storhet z, som själv är en funktion av en tredje storhet x, är tydligen y också en funktion av x. Man säger att y är en sammansatt funktion av x eller en funktion av en funktion av x:

y = ƒ(z), z = g(x) så är y = ƒ[g(x)] en sammansatt funktion av x, som betecknas även ƒ  g   (läses: cirkel ƒ, ƒ ring g eller ƒ boll g)
(ƒ ○ g)(x) = ƒ [g(x)]

Ex:

Funktion	Funktionsvärde	Definitionsområde
ƒ	ƒ(x)=	[0,∞]
g	g(x) = x + 1
ƒ  g	(ƒ  g)(x) = ƒ[g(x)] = ƒ(x+1) =	[-1,∞]
g  ƒ	(g  ƒ)(x) = g[ƒ(x)] = g() = + 1	[0,∞]
ƒ  ƒ	(ƒ  ƒ)(x) = ƒ[ƒ(x)] = ƒ() =	[0,∞]
g  g	(g  g)(x) = g[g(x)] = g(x+1) = (x+1)+1 = x+2

Funktioner av två variabler

z = ƒ(x, y)

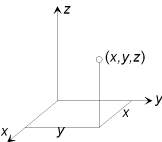För att åskådliggöra en funktion av två variabler behöver vi ett koordinatsystem med tre emot varandra vinkelräta axlar; en x-axel, en y-axel och en z-axel. Innebörden av en punkts koordinater (x, y, z) i detta s. k. rymdkoordinatsystem framgår av figuren. En funktion av en variabel betyder i allmänhet en kroklinje, belägen i ett plan. En funktion av två variabler kommer att betyda en yta i rymden.

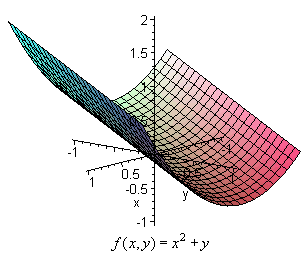
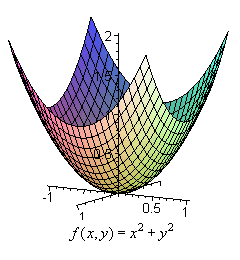
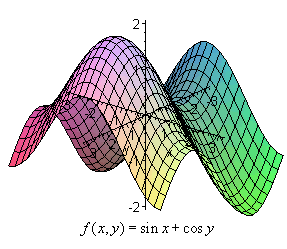
FORMEL

En formel är en med matematiska tecken uttryckt sats, regel.

Att lösa ut en obekant från en formel menar man omarbetning av formeln så att den sökta storheten kommer till vänsterledet och resten av obekanta samt konstanterna i högerledet.

T.ex. Gränsen av beviljad kredit är betyder inte att årslön är 12 · kreditgräns.