WolframAlpha| WolframAlpha |
Lexikon | Formler | Terminologi länkar | Svenska matematiklänkar | Math. Resources on the Internet | Böcker |
 Gästbok |
Nedladdning
|
|
| evolvent, evoluta | Spiraler |
Koordinatsystem i planet |
Spiral (snigelkurva) är en plan kurva som oändligt många gånger går runt en fix punkt och då antingen rör sig från punkten eller mot den.
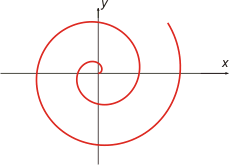
Arkimedes spiral den kurva som beskrivs när en punkt rör sig med konstant hastighet längs en rät linje som samtidigt roterar med jämn hastighet kring en fast punkt.Kurvan har den polära ekvationen r = a· φ, där a är en positiv konstant. |
 |
|
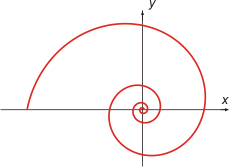
Logaritmisk spiral plan spiral som har den egenskapen att vinkeln mellan radien och tangenten i radiens ändpunkt på spiralen är lika stor i spiralens alla punkter Kurvan har den polära ekvationen
|
 |
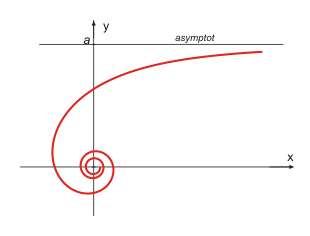
Hyperbolisk spiral plan spiral i vilken avståndet till centrum är omvänt proportionellt mot vinkeln φKurvans polära ekvationen:
|
 |
|
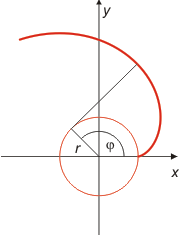
Cirkelevolvent Om en snöre är lindat runt en cirkel med radien r, kommer snörets ändpunkt att beskriva en evolvent, då det lindas av och hela tiden hålls sträckt.Kurvan i parameterform med parametern φ = vridningsvinkel:
|
 |
Evoluta
en kurva hos vilken alla tangenter är normaler till en annan kurva. Den kan också betraktas som sammanfattningen av (geometriska orten för) den andra kurvans krökningsmedelpunkter. Den andra kurvan benämnes evolvent till evoluta.
| av Bruno Kevius All kopiering tillåten! |
Matematiklexikon: A B C D E F G H I J K L M N O P Q R S T U V X Y z Ä Ö Klicka på någon av bokstäverna |
Svenska Matematiklänkar |
, där a > 0, b > 0
