WolframAlpha

Lexikon

Formler

Terminologi länkar

Svenska matematiklänkar

Math. Resources on the Internet

Böcker

Gästbok

Matematik minimum - Terminologi En alfabetisk klickbar lista över de vanligaste definitionerna och termerna inom matematik A  B  C  D  E  F  G  H  I  J  K  L  M  N  O  P  Q  R  S  T  U  V  X  Y  Z  Å  Ä  Ö      Klicka på någon av bokstäverna

Nedladdning

Ekvationer för räta linjen

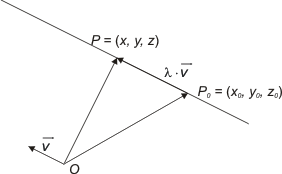En rät linje i rymden (i ett tredimensionella koordinatsystem) kan vara bestämd av t.ex. en punkt P0 och en vektor (ej nollvektor). Då gäller att en punkt P tillhör den räta linjen precis då vektorn är parallell med vektorn . Detta innebär att det finns ett tal λ så att = λ· Vektorn kallar vi en riktningsvektor för den räta linjen, och talet λ parameter för punkten P.

En linje som går genom en given punkt P₀(x₀, y₀, z₀), och har riktningsvektorn (a, b, c) har ekvationer som kan skrivas antingen som
(x, y, z) = (x₀, y₀, z₀) + λ·(a, b, c)
eller som
x = x₀ + λ·a
y = y₀ + λ·b
z = z₀ + λ·c
eller som

Vinkel mellan två räta linjer

Med vinkeln φ mellan två räta linjer menar vi vinkeln mellan två riktningsvektorer och ,en för vardera linjen. Eftersom skalärprodukten definierades genom · = |v₁|·|v₂|·cos φ, kan vi använda skalärprodukten för vinkelberäkningar.

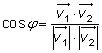
Exempel: Beräkna vinkeln mellan de räta linjerna
(x₁, y₁, z₁) = (1, 0, 3) + t₁(1, -1, 2) och
(x₂, y₂, z₂) = (0, 4, 4) + t₂(3, -1, 1)
då
vilket ger φ = 42,4º

Planets ekvation

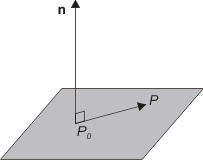En vektor som är ej nollvektor och som är vinkelrät mot varje vektor i ett plan kallas en normalvektor till planet. Genom att utgå från en fix punkt P0 i ett givet plan och en normalvektor till planet kan vi bestämma en ekvation för planet. Vi utnyttjar då att skalärprodukten av och är 0 för alla punkter P i planet. Ett plan som går genom en punkt P0(x0, y0, z0) och vars normaler är parallella med vektorn (a, b, c) har en ekvation a(x - x0) + b(y - y0) + c(z - z0) = 0 vilken också kan skrivas ax + by + cz + d = 0 där d = - (ax0 + by0 + cz0)

Skärning mellan två plan

En ekvation för skärningslinjen mellan två icke-parallella plan kan vi få genom att lösa det ekvationssystem som de båda planens ekvationer bildar. Två plan representeras av två förstagradsekvationer:

a₁x + b₁y + c₁z + d₁ = 0
a₂x + b₂y + c₂z + d₂ = 0

x =  + z
y =  + z

Med användning av en parameter λ får ekvationen för den räta linjen genom punkten P₀(x₀, y₀, z₀) med riktningscosinerna a, b, c formen:
x = x₀ + λ·a
y = y₀ + λ·b
z = z₀ + λ·c

x =  + t
y =  + t
z =    t

Vinkel mellan två plan

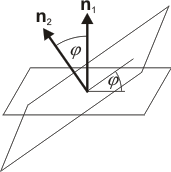Vinkeln φ mellan två plan får vi som vinkeln mellan två normalvektorer till planen. Numeriskt beräknar vi vinkeln med hjälp av skalärprodukten. n1·n2 = |n1|·|n2|·cos φ